某学习小组欲探究物体的加速度与力、质量的关系，他们在实验室组装了一套如图所示的装置，图中小车的质量用M表示，钩码的质量用m表示。要顺利完成该实验，则：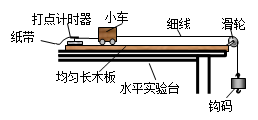
（1）还需要的测量工具有 、 。
（2）为使小车所受合外力等于细线的拉力，应采取的措施是 ；要使细线的拉力约等于钩码的总重力，应满足的条件是 （填M≈m、M≥m或M≤m）。
（3）在保持小车所受合外力一定的情况下，对实验得到的一系列纸带进行处理，测得小车加速度a与其质量M的数据如下表：（钩码质量m=30g）
| 实验次数 |
1 |
2 |
3 |
4 |
5 |
6 |
| a（m·s-2） |
1.51 |
1.23 |
1.00 |
0.86 |
0.75 |
0.67 |
| M （kg） |
0.20 |
0.25 |
0.30 |
0.35 |
0.40 |
0.45 |
| 1/M（kg-1） |
5.00 |
4.00 |
3.33 |
2.86 |
2.50 |
2.22 |
为了寻求a 与M间的定量关系，请利用表中数据在图示的直角坐标系中选取合适的横坐标及标度，并作出相应的图线。
如图所示，圆轨道AB是在竖直平面内的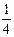
圆周，在B点轨道的切线是水平的，一质点自A点从静止开始下滑，不计摩擦和空气阻力，则在质点刚要到达B点时的加速度大小为，滑过B点时的加速度大小为。
如图所示的皮带传动装置中，右边两轮是连在一起同轴转动，图中三轮半径的关系为：r1=2r2，r3=1.5r1，A、B、C三点为三个轮边缘上的点，皮带不打滑，则A、B、C三点的线速度之比为。角速度之比为。周期之比为。
如图所示，定滑轮的半径r=2cm，绕在滑轮上的细线悬挂着一个重物，由静止开始释放，测得重物以加速度a=2m/s2做匀加速运动，在重物由静止下落距离为1 m的瞬间，滑轮边缘上的点的角速度ω=rad／s，向心加速度a=m/s2。（滑轮质量不计）
如图所示的电路中，电阻R1=1Ω，R2=2Ω，R3=3Ω，在A、B间接电源，S1、S2都打开，此时电阻R1、R2、R3消耗的功率之比P1：P2：P3=；当S1、S2都闭合时，电阻R1、R2、R3消耗的功率之比P'1：P'2：P'3=。
在图所示的8个不同的电阻组成，已知R1=12Ω，其余电阻值未知，测得A、B间的总电阻为4Ω，今将R1换成6Ω的电阻，A、B间总电阻变成Ω。