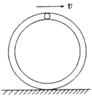
如图是利用传送带装运煤块的示意图.其中,传送带长L=20m,倾角θ=37°,煤块与传送带间的动摩擦因数μ=0.8,传送带的主动轮和从动轮半径相等,主动轮轴顶端与运煤车底板间的竖直高度H=1.8 m,与运煤车车箱中心的水平距离x=1.2 m.现在传送带底端由静止释放一些煤块(可视为质点)其质量为2kg,煤块在传送带的作用下先做匀加速直线运动,后与传送带一起做匀速运动,到达主动轮时随轮一起匀速转动.要使煤块在轮的最高点水平抛出并落在车箱中心,取g=10 m/s2,sin 37°=0.6,cos 37°=0.8,求:
(1)传送带匀速运动的速度v及主动轮和从动轮的半径r .(提示:要使煤块在轮的最高点做平抛运动,则煤块到达轮的最高点时对轮的压力为零)
(2)煤块在传送带上由静止开始加速至与传送带速度相同所经过的时间t.
(3传送带由于传送煤块多消耗多少电能? (提示:煤块传到顶端过程中,其机械能增加,煤块与传送带摩擦生热.)
一个LC振荡电路,电感L变化的范围是0.1~4.0mH,电容C的变化范 围是4~90PF,求此振荡电路的频率范围和产生的电磁波的波长范围
围是4~90PF,求此振荡电路的频率范围和产生的电磁波的波长范围
如图,折射率为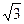 的玻璃球,被一束光线照射、若入射角
的玻璃球,被一束光线照射、若入射角 为60°,求:
为60°,求:
(1)入射处反射线和折射线的夹角
(2)光线从球射入空气的折射角。
(A组)如图所示,一质量为0. 5 kg的小球,用0. 4 m长的细线拴住,在竖直平面内做圆周运动,求:
(1)当小球在圆周最高点速度为4 m/s时,细线的拉力是多少?
(2)当小球在圆周最低点速度为6 m/s时,细线的拉力是多少?
(3)若绳子能承受的最大拉力为130 N,则小球运动到最低点时速度最大是多少?(g取10 m/s2 )
(B组)如图所示,质量为0.1kg的木桶内盛水0.5kg,用50c m的绳子系桶,使它在竖直平面内做圆周运动。如果通过最高点和最低点时的速度大小分别为8m/s和10m/s,求:木桶在最高点和最低点对绳的拉力和水对桶的压力。(g取10 m/s2 )
m的绳子系桶,使它在竖直平面内做圆周运动。如果通过最高点和最低点时的速度大小分别为8m/s和10m/s,求:木桶在最高点和最低点对绳的拉力和水对桶的压力。(g取10 m/s2 )
(A组)如图所示,定滑轮的半径r="2" cm,绕在滑轮上的细线悬挂着一个重物,由静止开始释放,测得重物以加速度a=2 m/s2做匀加速运动,在重物由静止下落距离为1 m的瞬间,求滑轮边缘上的点的角速度和向心加速度。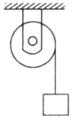
(B组)在竖直平面内有一个粗糙的1/4圆弧轨道,其半径R=0.4m,轨道的最低点距地面高度H=0.8m。 一质量m=0.1kg的小滑块从轨道的最高点由静止释放,到达最低点时以一定的水平速度离开轨道。落地点距轨道最低点的水平距离S=0.8m。空气阻力不计,g取10 m/s2,求:
(1)小滑块离开轨道时的速度大小;
(2)小滑块运动到B点时,小球对轨道的压力多大?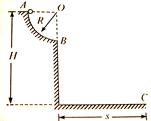
如图所示,小球质量为m,内壁光滑的导管弯成圆周轨道竖直放置,导轨质量为2m,让球在管内滚动,当小球运动到最高点时,导管刚好要离开地面,此时小球速度多大?(轨道半径为R)