在半径为R的某星球上,从高为h的平台上水平踢出一球,欲击中水平面上的A点,若两次踢球的方向都相同,第一次初速度为v1,着地点比A近了a,第二次初速度为v2,着地点却比A远了b,已知万有引力常量为G,求该星球的质量。
质点从静止开始做匀加速直线运动,经4s后速度达到20m/s,然后匀速运动了10s,接着经4s匀减速运动后静止。
求(1)质点在加速运动阶段和减速阶段的加速度有多大?
(2)质点在整个过程的平均速度是多大?
(12分)如图所示的电路中,电源电动势E=10V,电阻R1=2.5Ω,R2=3Ω,当电阻箱Rx调到3Ω时,电流表的示数为2 A.(电表理想处理)求: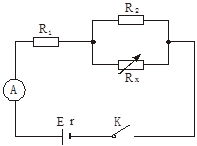
(1)电源的内电阻;
(2)调节电阻箱,使电流表的示数为1.6A时,电阻R2消耗的电功率。
(10分)电动玩具汽车的直流电动机电阻一定,当加上0.3V电压时,通过的电流为0.3A,此时电动机没有转动。当加上3V 电压时,电流为1A,这时候电动机正常工作。求
(1)电动机的电阻;
(2)电动机正常工作时,产生的机械功率和发热功率。
(10分)把一个带电荷量2×10﹣8C的正点电荷从无限远处移到电场中A点时,要克服电场力做功8×10﹣6J,若把该电荷从无限远处移到电场中B点,需克服电场力做功2×10﹣6J,取无限远处电势为零。求:
(1)A点的电势;
(2)A、B两点的电势差;
(3)若把2×10﹣5C的负电荷由A点移到B点电场力做的功。
某校举行托乒乓球跑步比赛,赛道为水平直道,比赛距离为S,比赛时,某同学将球置于球拍中心,以大小a的加速度从静止开始做匀加速运动,当速度达到v0时,再以v0做匀速直线运动跑至终点。整个过程中球一直保持在球中心不动。比赛中,该同学在匀速直线运动阶级保持球拍的倾角为θ0 ,如题25图所示。设球在运动过程中受到的空气阻力与其速度大小成正比,方向与运动方向相反,不计球与球拍之间的摩擦,球的质量为m,重力加速度为g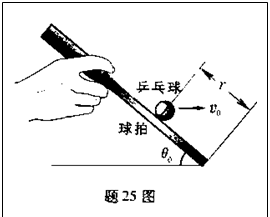
⑴空气阻力大小与球速大小的比例系数k
⑵求在加速跑阶段球拍倾角θ随球速v变化的关系式
⑶整个匀速跑阶段,若该同学速率仍为v0,而球拍的倾角比θ0大了β并保持不变,不计球在球拍上的移动引起的空气阻力的变化,为保证到达终点前球不从球拍上距离中心为r的下边沿掉落,求β应满足的条件。