为了应对国际原油的变化，某地建设一座油料库。现在油料库已储油料
吨，计划正式运营后的第一年进油量为已储油量的
，以后每年的进油量为上一年年底储油量的，且每年运出
吨，设
为正式运营第n年年底的储油量。（其中
）
（1）求的表达式
（2）为应对突发事件，该油库年底储油量不得少于
吨，如果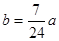
吨，该油库能否长期按计划运营？如果可以请加以证明；如果不行请求出最多可以运营几年。（取
）
已知函数
（I）求函数
的最小正周期；
（II）求函数
上的最大值与最小值.
已知等差数列
的每一项都有
求数列
的前n项和
在数列
和
中，
，
，
，其中
且
，
．设
，
，试问在区间
上是否存在实数
使得
．若存在，求出的一切可能的取值及相应的集合
；若不存在，试说明理由．
学校文娱队的每位队员唱歌、跳舞至少会一项，已知会唱歌的有2人，会跳舞的有5人，现从中选2人．设
为选出的人中既会唱歌又会跳舞的人数，且
．
（1）求文娱队的队员人数；
（2）写出的概率分布列并计算
在直角坐标系
中，直线
的参数方程为
（
为参数），若以直角坐标系
的
点为极点，
为极轴，且长度单位相同，建立极坐标系，得曲线
的极坐标方程为
．
（1）求直线的倾斜角；
（2）若直线与曲线交于
两点，求