某学生站在公园湖边的M处,测得湖心亭A位于北偏东30°方向上,又测得游船码头B位于南偏东60°方向上.现有一艘游船从湖心亭A 处沿正南方向航行返回游船码头,已知M处与AB的距离MN=0.7千米,求湖心亭与游船码头B的距离(精确到0.1千米).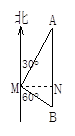
在一个箱子中放有三张完全相同的卡片,卡片上分别标有数字1,2,3.从箱子中任意取出一张卡片,用卡片上的数字作为十位数字,放回后搅匀,再取出一张卡片,用卡片上的数字作为个位数字,这样组成一个两位数.
(1)请你用画树状图或列表的方法表示所有等可能的结果;
(2)组成的两位数是偶数的概率是多少?
为了测量树的高度HD,在离树20米的C处,用高1.20米的测角仪AC测得树顶端H的仰角为35°,求树HD的高.(精确到0.1米)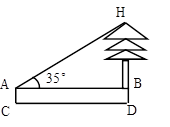
解方程: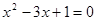
计算: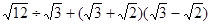
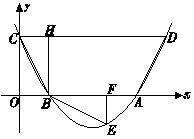
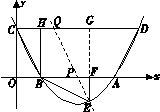
如图,抛物线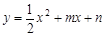 与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.
与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.
求(1)求C点的坐标及抛物线的解析式;
(2)将△BCH绕点B按顺时针旋转90°后 再沿x轴对折得到△BEF(点C与点E对应),判断点E是否落在抛物线上,并说明理由;
(3)设过点E的直线交AB边于点P,交CD边于点Q. 问是否存在点P,使直线PQ分梯形ABCD的面积为1∶3两部分?若存在,求出P点坐标;若不存在,请说明理由.