已知:直线y=-2x-2与x轴交于点A,与y轴交于点C,抛物线经过点A、C、E,且点E(6,7)
(1)求抛物线的解析式.
(2)在直线AE的下方的抛物线取一点M使得构成的三角形AME的面积最大,请求出M点的坐标及△AME的最大面积.
(3)若抛物线与x轴另一交点为B点,点P在x轴上,点D(1,-3),以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.
某公司市场营销部的营销员的个人月收入与该营销员每月的销量成一次函数关系,其图象如图8所示. 根据图象提供的信息,解答下列问题:求出营销人员的个人月收入y元与该营销员每月的销售量x万件(x≥0)之间的函数关系式;
该公司营销人员的底薪是(没有销售量时的收入)多少元?
已知该公司营销员李明5月份的销售量为1.2万件,求李明5月份的收入.
现要装配30台机器,在装配好6台后,采用了新的技术,每天的工作效率提高了一倍,结果共用了3天完成了任务. 求采用新的技术后每天能装多少台机器.
先化简,再求值: ,其中
,其中 .
.
请从下列三个代数式中任选两个构造一个分式,并化简该分式. ,
,  ,
,  .
.
已知,如图,二次函数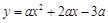
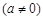 图象的顶点为
图象的顶点为 ,与
,与 轴交于
轴交于 、
、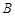 两点(
两点(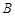 在
在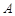 点右侧),点
点右侧),点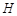 、
、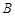 关于直线
关于直线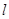 :
: 对称
对称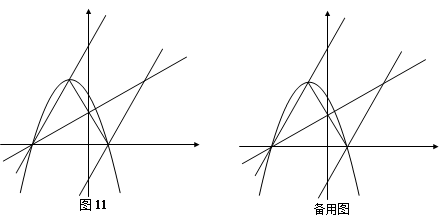
求
 、
、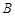 两点坐标,并证明点
两点坐标,并证明点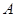 在直线
在直线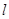 上
上求二次函数解析式;
过点
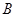 作直线
作直线 ∥
∥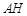 交直线
交直线 于
于 点,
点,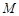 、N分别为直线
、N分别为直线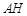 和直线
和直线 上的两个动点,连接
上的两个动点,连接 、
、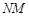 、
、 ,求
,求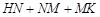 和的最小值.
和的最小值.