如图，经过原点的抛物线
与
轴的另一个交点为A．过点
作直线
轴于点M，交抛物线于点B，过点B作直线BC∥轴与抛物线交于点C（B、C不重合），连结CP．
（1）当
时，求点A的坐标及BC的长；
（2）当
时，连结CA，问
为何值时
？
（3）过点P作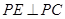
且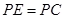
，问是否存在，使得点E落在坐标轴上？若存在，求出所有满足要求的的值，并求出相对应的点E坐标；若不存在，请说明理由．
已知
，且
，求
的值．
某服装厂生产一种西装和领带，西装每套定价200元，领带每条定价40元。厂方在开展促销活动期间，向客户提供两种优惠方案：①买一套西装送一条领带；②西装和领带都按定价的90%付款．现某客户要到该服装厂购买西装20套，领带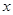
条（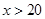
）．
（1）若该客户按方案①购买，需付款元（用含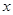的代数式表示）;
若该客户按方案②购买，需付款元（用含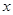的代数式表示）．
（2）请你通过计算帮该顾客设计较为合算购买方案？
如图，已知∠AOB是直角，∠BOC＝600， OE平分∠AOC，OF平分∠BOC．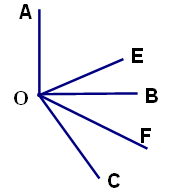
（1）求∠EOF的度数；
（2）若将条件“∠AOB是直角，∠BOC＝600”改为： ∠AOB＝ x0，∠EOF＝y0，条件不变．
①则请用x的代数式来表示y．
②如果∠AOB+∠EOF＝1560．则∠EOF是多少度？
如图，一副三角板的两个直角顶点重合在一起．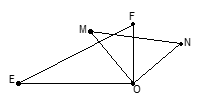
（1）比较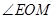
与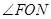
的大小，并说明理由；
（2）
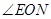与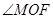
的和为多少度？为什么？
一个角的补角加上24º，恰好等于这个角的5倍，求这个角的度数．