一个质量为m、电量为+q的小球,用丝线悬挂在水平方向的匀强电场中,场强为E,平衡时悬线与竖直方向间夹角α="30" °(如图所示),若将匀强电场E的方向逆时针转过角度β=45°,小球重新平衡时悬线与竖直方向间夹角正切为多大?(可以保留根号)
汽车以1.6m/s的速度在水平地面上匀速行驶,汽车后壁货架上放有一小球(可视作质点),架高1.8 m。由于前方事故,突然急刹车,汽车轮胎抱死,小球从架上落下。已知该型号汽车在所在路面行驶时刹车痕s (即刹车距离)与刹车前车速v的关系如下图线所示,忽略货物与架子间的摩擦及空气阻力,g取10m/s2。求:
(1)汽车刹车过程中的加速度多大;
(2)货物在车厢底板上落点距车后壁的距离.
如图所示的水平转盘可绕竖直轴OO′旋转,盘上水平杆上穿着两个质量均为m=2kg的小球A和B。现将A和B分别置于距轴rA=0.5m和rB=1m处,并用不可伸长的轻绳相连。已知两球与杆之间的最大静摩擦力都是fm=1N。试分析转速ω从零缓慢逐渐增大(短时间内可近似认为是匀速转动),两球对轴保持相对静止过程中,在满足下列条件下,ω的大小。
(1)绳中刚要出现张力时的ω1;
(2)A、B中某个球所受的摩擦力刚要改变方向时的ω2,并指明是哪个球的摩擦力方向改变;
(3)两球对轴刚要滑动时的ω3。
如图所示,质量为m的木块从A点水平抛出,抛出点离地面高度为l,不计空气阻力,在无风情况下落地点B到抛出点的水平距离为s;当有恒定的水平风力F时,仍以原来初速度抛出,落地点C到抛出点的水平距离为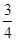 s。试求:
s。试求: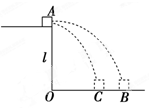
(1)无风情况下木块落地时的速度大小;
(2)水平风力F的大小。
A、B是在真空中水平正对的两块金属板,板长L=40cm,板间距d=24cm,在B板左侧边缘有一粒子源,能连续均匀发射带负电的粒子,粒子紧贴B板水平向右射入,如图甲所示,带电粒子的比荷为 =1.0×108C/kg,初速度v0=2×105m/s(粒子重力不计),在A、B两板间加上如图乙所示的电压,电压的周期T=2.0×10-6s,t=0时刻A板电势高于B板电势,两板间电场可视为匀强电场,电势差U0=360V,A、B板右侧相距s=2cm处有一边界MN,在边界右侧存在一垂直纸面向里的匀强磁场,磁感应强度B=
=1.0×108C/kg,初速度v0=2×105m/s(粒子重力不计),在A、B两板间加上如图乙所示的电压,电压的周期T=2.0×10-6s,t=0时刻A板电势高于B板电势,两板间电场可视为匀强电场,电势差U0=360V,A、B板右侧相距s=2cm处有一边界MN,在边界右侧存在一垂直纸面向里的匀强磁场,磁感应强度B= T,磁场中放置一“>”型荧光板,位置如图所示,板与水平方向夹角θ=37°,不考虑粒子之间相互作用及粒子二次进入磁场的可能,求:
T,磁场中放置一“>”型荧光板,位置如图所示,板与水平方向夹角θ=37°,不考虑粒子之间相互作用及粒子二次进入磁场的可能,求:
⑴带电粒子在AB间偏转的最大侧向位移ymax;
⑵带电粒子从电场中射出到MN边界上的宽度Δy;
⑶经过足够长时间后,射到荧光板上的粒子数占进入磁场粒子总数的百分比k。
倾斜的传送带以恒定的速率沿逆时针方向运行,如图甲所示,在t=0时,将质量m=2.0kg的小物块轻放在传送带上A点处,2s时物块从B点离开传送带,物块速度随时间变化的图象如图乙所示,设沿传送带向下为运动的正方向,取重力加速度g=10m/s2。求:
⑴0~1s内物块所受的合外力大小;
⑵小物块与传送带之间的动摩擦因数;
⑶在0~2s内由于小物块与皮带间的摩擦所产生的热量。