我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释,例如:图A
可以用来解释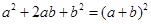 ,实际上利用一些卡片拼成的图形面积也可以
,实际上利用一些卡片拼成的图形面积也可以
对某些二次三项式进行因式分解.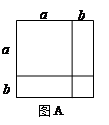
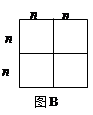

(1)图B可以解释的代数恒等式是_____________;
(2)现有足够多的正方形和矩形卡片,如图C:
①.若要拼出一个面积为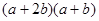 的矩形,则需要1号卡片张,2号卡片张,
的矩形,则需要1号卡片张,2号卡片张,
3号卡片张;
②.试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的矩形,使该矩形的面积为 ,并利用你画的图形面积对
,并利用你画的图形面积对 进行因式分解.
进行因式分解.
如图,在等腰梯形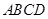 中,
中,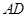 ∥
∥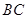 ,已知
,已知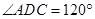 ,
,
(1)求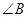 的度数;
的度数;
(2)若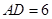 ,
,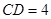 ,试求等腰梯形
,试求等腰梯形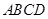 的周长.
的周长.
某校生物兴趣小组有一块正方形种植基地,现要对它进行扩建,若把边长增加2米,则所得的新正方形种植基地面积比原来增加了32平方米,求:原来正方形种植基地的边长是多少?
如图,已知菱形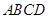 的周长为52cm,对角线
的周长为52cm,对角线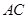 、
、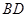 交于点
交于点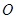 ,且
,且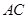 =10,
=10,
试求菱形的边长与面积.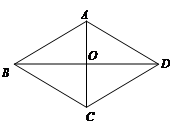
如图,在正方形网格中每个小正方形的边长都是单位长度1,△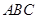 的顶点都在格点上,且△
的顶点都在格点上,且△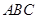 与△
与△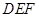 关于点
关于点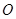 成中心对称.
成中心对称.
(1)在网格图中标出对称中心点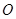 的位置;
的位置;
(2)画出将△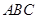 沿水平方向向右平移5个单位后的△
沿水平方向向右平移5个单位后的△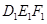 .
.