如图①,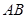 为⊙
为⊙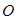 的直径,
的直径,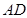 与⊙
与⊙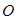 相切于点
相切于点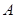 ,
, 与⊙
与⊙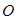 相切于点
相切于点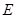 ,点
,点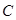 为
为 延长线上一点,且CE=CB.
延长线上一点,且CE=CB.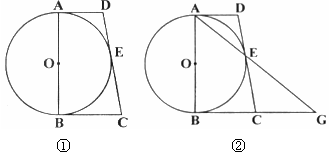
(1)求证: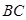 为⊙
为⊙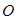 的切线;
的切线;
(2)如图②,连接AE,AE的延长线与BC的延长线交于点G.若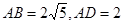 ,求线段BC和EG的长.
,求线段BC和EG的长.
(内江)如图,抛物线与x轴交于点A( ,0)、点B(2,0),与y轴交于点C(0,1),连接BC.
,0)、点B(2,0),与y轴交于点C(0,1),连接BC.
(1)求抛物线的函数关系式;
(2)点N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t( ),求△ABN的面积S与t的函数关系式;
),求△ABN的面积S与t的函数关系式;
(3)若 且
且 时△OPN∽△COB,求点N的坐标.
时△OPN∽△COB,求点N的坐标.
(达州)学校为了奖励初三优秀毕业生,计划购买一批平板电脑和一批学习机,经投标,购买1台平板电脑比购买3台学习机多600元,购买2台平板电脑和3台学习机共需8400元.
(1)求购买1台平板电脑和1台学习机各需多少元?
(2)学校根据实际情况,决定购买平板电脑和学习机共100台,要求购买的总费用不超过168000元,且购买学习机的台数不超过购买平板电脑台数的1.7倍.请问有哪几种购买方案?哪种方案最省钱?
(达州)如图,在平面直角坐标系中,四边形ABCD是菱形,B.O在x轴负半轴上,AO= ,tan∠AOB=
,tan∠AOB= ,一次函数
,一次函数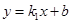 的图象过A、B两点,反比例函数
的图象过A、B两点,反比例函数 的图象过OA的中点D.
的图象过OA的中点D.
(1)求一次函数和反比例函数的表达式;
(2)平移一次函数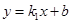 的图象,当一次函数
的图象,当一次函数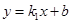 的图象与反比例函数
的图象与反比例函数 的图象无交点时,求b的取值范围.
的图象无交点时,求b的取值范围.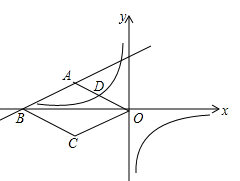
(达州)阅读与应用:阅读1:a、b为实数,且a>0,b>0,因为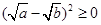 ,所以
,所以 从而
从而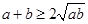 (当a=b时取等号).
(当a=b时取等号).
阅读2:若函数 ;(m>0,x>0,m为常数),由阅读1结论可知:
;(m>0,x>0,m为常数),由阅读1结论可知: ,所以当
,所以当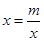 ,即
,即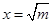 时,函数
时,函数 的最小值为
的最小值为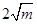 .
.
阅读理解上述内容,解答下列问题:
问题1:已知一个矩形的面积为4,其中一边长为x,则另一边长为 ,周长为2(
,周长为2( ),求当x= 时,周长的最小值为 ;
),求当x= 时,周长的最小值为 ;
问题2:已知函数 (
(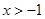 )与函数
)与函数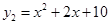 (
(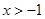 ),
),
当x= 时, 的最小值为 ;
的最小值为 ;
问题3:某民办学校每天的支出总费用包含以下三个部分:一是教职工工资4900元;二是学生生活费成本每人10元;三是其他费用.其中,其他费用与学生人数的平方成正比,比例系数为0.01.当学校学生人数为多少时,该校每天生均投入最低?最低费用是多少元?(生均投入=支出总费用÷学生人数)
(达州)在△ABC的外接圆⊙O中,△ABC的外角平分线CD交⊙O于点D,F为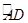 上一点,且
上一点,且 连接DF,并延长DF交BA的延长线于点E.
连接DF,并延长DF交BA的延长线于点E.
(1)判断DB与DA的数量关系,并说明理由;
(2)求证:△BCD≌△AFD;
(3)若∠ACM=120°,⊙O的半径为5,DC=6,求DE的长.