设关于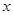 的一元二次方程
的一元二次方程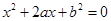 .
.
(1)若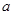 ,
, 都是从集合
都是从集合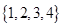 中任取的数字,求方程有实根的概率;
中任取的数字,求方程有实根的概率;
(2)若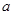 是从区间[0,4]中任取的数字,
是从区间[0,4]中任取的数字, 是从区间[1,4]中任取的数字,求方程有实根的概率.
是从区间[1,4]中任取的数字,求方程有实根的概率.
如图,三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=2,AC=6,点D在线段BB1上,且BD= ,A1C∩AC1=E.
,A1C∩AC1=E.
(Ⅰ)求证:直线DE与平面ABC不平行;
(Ⅱ)设平面ADC1与平面ABC所成的锐二面角为θ,若cosθ= ,求AA1的长;
,求AA1的长;
(Ⅲ)在(Ⅱ)的条件下,设平面ADC1∩平面ABC=l,求直线l与DE所成的角的余弦值.
已知数列{an}的前n项和为Sn,且a1= .
.
(1)求{an}的通项公式;
(2)设bn=n(2﹣Sn),n∈N*,若bn≤λ,n∈N*恒成立,求实数λ的取值范围.
(3)设Cn= ,Tn是数列{Cn}的前n项和,证明
,Tn是数列{Cn}的前n项和,证明 ≤Tn<1.
≤Tn<1.
设函数f(x)=cos(2x﹣ )+2cos2x,
)+2cos2x,
(Ⅰ)求f(x)的最大值,并写出使f(x)取最大值时x的集合;
(Ⅱ)已知△ABC中,角A、B、C的对边分别为a、b、c,若f(B+C)= ,b+c=2,a=1,求△ABC的面积的最大值.
,b+c=2,a=1,求△ABC的面积的最大值.
【选修4-5:不等式选讲】
(1)设函数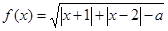 的定义域为
的定义域为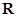 ,试求
,试求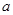 的取值范围;
的取值范围;
(2)已知实数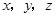 满足
满足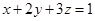 ,求
,求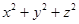 的最小值.
的最小值.
【选修4-4:坐标系与参数方程】
已知曲线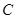 的参数方程为:
的参数方程为: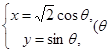 为参数),直线
为参数),直线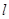 的参数方程为:
的参数方程为: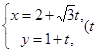 为参数),点
为参数),点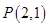 ,直线
,直线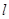 与曲线
与曲线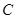 交于
交于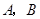 两点.
两点.
(1)写出曲线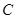 和直线
和直线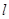 在直角坐标系下的标准方程;
在直角坐标系下的标准方程;
(2)求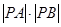 的值.
的值.