已知斜三棱柱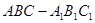 的各棱长均为2, 侧棱
的各棱长均为2, 侧棱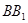 与底面
与底面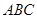 所成角为
所成角为 ,且侧面
,且侧面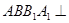 底面
底面 .
.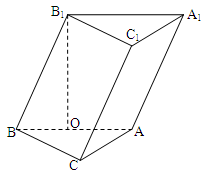
 (1)证明:点
(1)证明:点 在平面
在平面 上的射影
上的射影 为
为 的中点;
的中点;


 (2)求二面角
(2)求二面角 的大小;
的大小;
(3)求点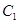 到平面
到平面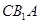 的距离.
的距离.
(本题满分16分,第1小题满分4分,第2小题的①满分6分,②满分6分.)
如图,椭圆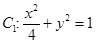 ,
, 轴被曲线
轴被曲线 截得的线段长等于
截得的线段长等于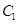 的长半轴长.
的长半轴长.
(1)求实数 的值;
的值;
(2)设 与
与 轴的交点为
轴的交点为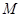 ,过坐标原点
,过坐标原点 的直线
的直线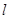 与
与 相交于点
相交于点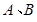 ,直线
,直线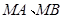
分别与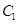 相交与
相交与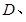
 .
.
①证明:
②记△ ,△
,△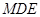 的面积分别是
的面积分别是 .若
.若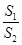 =
= ,求
,求 的取值范围.
的取值范围.
如图所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下球状液体,其中球状液体的半径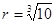 毫米,滴管内液体忽略不计.
毫米,滴管内液体忽略不计.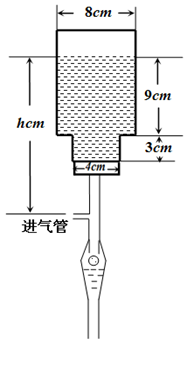
(1)如果瓶内的药液恰好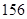 分钟滴完,问每分钟应滴下多少滴?
分钟滴完,问每分钟应滴下多少滴?
(2)在条件(1)下,设输液开始后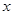 (单位:分钟),瓶内液面与进气管的距离为
(单位:分钟),瓶内液面与进气管的距离为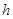 (单位:厘米),已知当
(单位:厘米),已知当 时,
时, .试将
.试将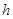 表示为
表示为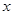 的函数.(注:
的函数.(注: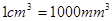 )
)
(本题满分14分,第1小题满分6分,第2小题满分8分).
已知向量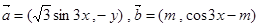
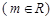 ,且
,且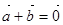 . 设
. 设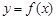 .
.
(1)求 的表达式,并求函数
的表达式,并求函数 在
在 上图像最低点
上图像最低点 的坐标.
的坐标.
(2)若对任意 ,
,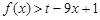 恒成立,求实数
恒成立,求实数 的范围.
的范围.
(本题满分12分;第1小题6分,第2小题6分)
已知函数
(1)若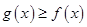 ,求
,求 的取值范围;
的取值范围;
(2)求 的最大值.
的最大值.
(本小题满分10分)
已知函数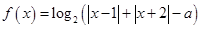 .
.
(1)当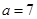 时,求函数
时,求函数 的定义域;
的定义域;
(2)若关于 的不等式
的不等式 的解集是
的解集是 ,求
,求 的取值范围.
的取值范围.