（本题10分）如图，矩形OBCD的边OD、OB分别在x轴正半轴和y轴负半轴上，且OD＝10，OB＝8．将矩形的边BC绕点B逆时针旋转，使点C恰好与x轴上的点A重合．
(1)直接写出点A、B的坐标：A( ， )、B( ， )；
(2)若抛物线y＝－
x2＋bx＋c经过点A、B，请求出这条抛物线的解析式；
(3)当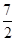
≤x≤7，在抛物线上存在点P，使△ABP的面积最大，那么△ABP最大面积是 ．（请直接写出结论，不需要写过程）
列方程或方程组解应用题：
A、B两地相距15千米，甲从A地出发步行前往B地，15分钟后，乙从B地出发骑车前往A地，且乙骑车的速度是甲步行速度的3倍．乙到达A地后停留45分钟，然后骑车按原路原速返回，结果甲、乙二人同时到达B地．求甲步行的速度．
如图，在平面直角坐标系xOy中，一次函数
的图象与x轴交于点A，与y轴交于点B，已知
，
，点C（-2，m）在直线AB上，反比例函数
的图象经过点C．
（1）求一次函数及反比例函数的解析式；
（2）结合图象直接写出：当
时，不等式
的解集．
已知
，求
的值．
已知：如图，点E、F在线段AD上，AE=DF，AB∥CD，∠B =∠C．
求证：BF =CE．
解不等式
，并把它的解集在数轴上表示出来．