一般的曲线运动可以分成很多小段,每小段都可以看成圆周运动的一部分,即把整条曲线用一系列不同半径的小圆弧来代替。如图甲所示,曲线上A点的曲率圆定义为:在曲线上某一点A和邻近的另外两点分别做一圆,当邻近的另外两点无限接近A点时,此圆的极限位置叫做曲线A点处的曲率圆,其曲率圆半径R叫做A点的曲率半径。现将一物体沿与水平面成θ角的方向以速度v0抛出,如图乙所示。不计空气阻力,则在其轨迹最高点P处的曲率半径r是( )
A. |
B. |
C. |
D. |
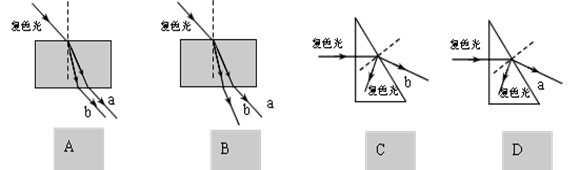
现让a、b两种光组成的复色光穿过平行玻璃砖或三棱镜时,光的传播方向中可能正确的是
两个振动情况完全一样的波源S1和S2相距6m,它们在空间产生的干涉图样如图所示,图中实线表示振动加强的区域,虚线表示振动减弱的区域。下列说法正确的是()
| A.两波源的振动频率一定相同 |
| B.虚线一定是波谷与波谷相遇处 |
| C.两列波的波长都是2m |
| D.两列波的波长都是1m |
关于多普勒效应,下列说法中正确的是:
| A.若波源相对介质不动,观察者远离波源,则接收到的频率小于波源发出的频率 |
| B.只要观察者相对地面运动,就一定可以出现多普勒效应 |
| C.若观察者相对介质不动,波源运动时,空间传播的波长发生变化 |
| D.若观察者相对介质不动,波源远离观察者时,观察者接收到的频率大于波源发出的频率 |
如图所示,顶端装有定滑轮斜面体放在粗糙水平地面上,A、B两物体通过细绳连接,整个装置处于静止状态(绳的质量和形变、绳与滑轮间的摩擦均不计)。现对物体B施加一水平向右的力F作用,使其拉高一定距离(斜面体与物体A仍然保持静止)。则在此过程中( ) 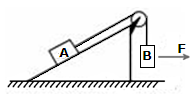
A. 若物体B缓慢移动,则地面对斜面体的摩擦力一定逐渐变大
B. 若物体B缓慢移动,则斜面体对物体A的摩擦力一定逐渐变大
C. 若水平拉力F为恒力,则地面对斜面体的摩擦力一定也为恒力
D. 水平拉力F所做的功一定等于物体A、B系统的机械能增量
如图所示,在真空中A、B两块平行金属板竖直放置并接入电路。调节滑动变阻器,使A、B两板间的电压为U时,一质量为m,电荷量为-q的带电粒子,以初速度v0从A板上的中心小孔沿垂直两板的方向射入电场中,恰从A、B两板的中点处沿原路返回(不计重力),则下列说法正确的是()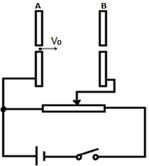
A.使初速度变为2 v0时,带电粒子恰能到达B板
B.使初速度变为2 v0时,带电粒子将从B板中心小孔射出
C.使初速度v0和电压U都增加为原来的2倍时,带电粒子恰能到达B板
D.使初速度v0和电压U都增加为原来的2倍时,带电粒子将从B板中心小孔射出