如图所示,小木块的品质为m,可看成质点,木板质量为M=2m,长度为l,一根质量不计的轻绳通过定滑轮分别与M和m连接,小木块与木板间以及木板与水平面间的动摩擦因子均为 ,开始时木块静止在木板左端。现用水平向右的恒力将木块拉至木板右端,则
,开始时木块静止在木板左端。现用水平向右的恒力将木块拉至木板右端,则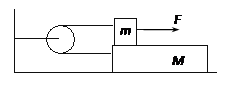
A.拉力至少为4 mg mg |
B.拉力至少为5 mg mg |
C.拉力至少做功5 mgl mgl |
D.拉力至少做功2.5 mgl mgl |
(多选)下列说法正确的是( )
A.据R= 可知,加在电阻两端的电压变为原来的2倍时,导体的电阻也变为原来的2倍 可知,加在电阻两端的电压变为原来的2倍时,导体的电阻也变为原来的2倍 |
| B.不考虑温度对阻值的影响,通过导体的电流及加在两端的电压改变时导体的电阻不变 |
C.据ρ=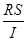 可知,导体的电阻率与导体的电阻和横截面积的乘积RS成正比,与导体的长度l成反比 可知,导体的电阻率与导体的电阻和横截面积的乘积RS成正比,与导体的长度l成反比 |
| D.导体的电阻率与导体的长度l、横截面积S、导体的电阻R皆无关 |
功率为10 W的发光二极管(LED灯)的亮度与功率为60 W的白炽灯相当。根据国家节能战略,2016年前普通白炽灯应被淘汰。假设每户家庭有2只60 W的白炽灯,均用10 W的LED灯替代,估算出全国一年节省的电能最接近( )
| A.8×108 kW·h | B.8×1010 kW·h | C.8×1011 kW·h | D.8×1013 kW·h |
一只电饭煲和一台洗衣机并联接在输出电压220 V的交流电源上(其内电阻可忽略不计),均正常工作。用电流表分别测得通过电饭煲的电流是5.0 A,通过洗衣机电动机的电流是0.50 A,则下列说法中正确的是( )
| A.电饭煲的电阻为44 Ω,洗衣机电动机线圈的电阻为440 Ω |
| B.电饭煲消耗的电功率为1 555 W,洗衣机电动机消耗的电功率为155.5 W |
| C.1 min内电饭煲消耗的电能为6.6×104 J,洗衣机电动机消耗的电能为6.6×103 J |
| D.电饭煲发热功率是洗衣机电动机发热功率的10倍 |
如图所示为一未知电路,现测得两个端点a、b之间的电阻为R,若在a、b之间加上电压U,测得通过电路的电流为I,则该未知电路的电功率一定为( )
| A.I2R | B.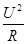 |
C.UI | D.UI-I2R |
两位同学穿旱冰鞋,面对面站立不动,互推后向相反的方向运动,不计摩擦阻力,下列判断正确的是
| A.互推后两同学总动量增加 |
| B.互推后两同学动量大小相等,方向相反 |
| C.分离时质量大的同学的速度小一些 |
| D.互推过程中机械能守恒 |