(本小题满分16分)
已知函数 ,
,
(1)若 在
在 上的最大值为
上的最大值为 ,求实数
,求实数 的值;
的值;
(2)若对任意 ,都有
,都有 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)在(1)的条件下,设 ,对任意给定的正实数
,对任意给定的正实数 ,曲线
,曲线 上是否存在两点
上是否存在两点 ,使得
,使得 是以
是以 (
( 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在 轴上?请说明理由。
轴上?请说明理由。
(本小题14分)
数列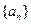 的前
的前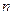 项和为
项和为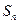 ,且对
,且对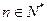 都有
都有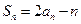 ,则:
,则:
(1)求数列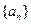 的前三项
的前三项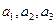 ;
;
(2)根据 上述结果,归纳猜想数列
上述结果,归纳猜想数列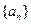 的通项
的通项 公式,并用数学归纳法加以证明.
公式,并用数学归纳法加以证明.
(3)求证:对任意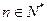 都有
都有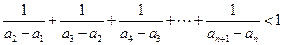 .
.
(本小题满分13分)
(1)3人坐在有八个座位的一排上,若每人的左右两边都要有空位,则不同坐法的种数为几种?
(2 )有5个人并排站成一排,如果甲必须在乙的右边,则不同的排法有
)有5个人并排站成一排,如果甲必须在乙的右边,则不同的排法有 多少种?
多少种?
(3)现有10个保送上大学的名额,分配给7所学校,每校至少有1个名额,问名额分配的方法共有多少种?
(本小题满分13分)
已知定义域为R的函数 是奇函数.
是奇函数.
(1)求a的值;(2)判断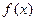 的单调性(不需要写出理由);
的单调性(不需要写出理由);
(3)若对任意的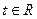 ,不等式
,不等式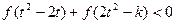 恒成立,求
恒成立,求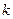 的取
的取 值范
值范 围.
围.
(本小题满分13分)
由0,1,2,3,4,5这六个数字
(1)能组成多少个无重复数字的四位数?
(2)能组成多少个无重复数字的四位偶数?
(3)能组成多少个无重复数字且被25整除的四位数?
(4)组成无重复数字的四位数中比4032大的数有多少个?
(本小题满分12分)
已知y=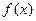 是二次函数,且f(0)=8及f(x+1)-f(x)=-2x+1
是二次函数,且f(0)=8及f(x+1)-f(x)=-2x+1
(1)求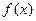 的解析式;
的解析式;
(2)求函数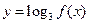 的单调递减区间及值域..
的单调递减区间及值域..