甲、乙两果园分别产有苹果10吨和40吨,现全部运送到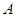 、
、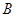 两地销售,根据市场调研,
两地销售,根据市场调研,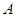 、
、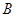 两地分别需要苹果15吨和35吨;已知从甲、乙地到
两地分别需要苹果15吨和35吨;已知从甲、乙地到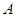 、
、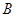 地的运价如表,由以上信息,解决下列问题:
地的运价如表,由以上信息,解决下列问题:
| |
到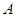 地运价 地运价 |
到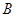 地运价 地运价 |
| 甲果园 |
150元∕吨 |
120元∕吨 |
| 乙果园 |
100元∕吨 |
90元∕吨 |
(1) 若从乙果园运到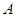 地的苹果为
地的苹果为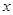 吨,则从甲果园运到
吨,则从甲果园运到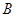 地的苹果为 吨;从甲果园将苹果运往
地的苹果为 吨;从甲果园将苹果运往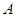 地的运输费用为 元(用含
地的运输费用为 元(用含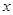 的代数式表示);
的代数式表示);
(2)若运往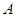 地的运输费用比运往
地的运输费用比运往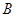 地的运输费用少1150元,用你所学的知识来说明是怎样安排运输方案的?
地的运输费用少1150元,用你所学的知识来说明是怎样安排运输方案的?