如图, ,
, 是抛物线
是抛物线 (
( 为正常数)上的两个动点,直线AB与x轴交于点P,与y轴交于点Q,且
为正常数)上的两个动点,直线AB与x轴交于点P,与y轴交于点Q,且

(Ⅰ)求证:直线AB过抛物线C的焦点;
(Ⅱ)是否存在直线AB,使得 若存在,求出直线AB的方程;若不存在,请说明理由。
若存在,求出直线AB的方程;若不存在,请说明理由。
已知命题 :复数
:复数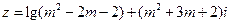 对应的点落在复平面的第二象限;命题
对应的点落在复平面的第二象限;命题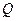 :以
:以 为首项,公比为
为首项,公比为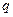 的等比数列的前
的等比数列的前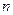 项和极限为2.若命题“
项和极限为2.若命题“ 且
且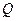 ”是假命题,“
”是假命题,“ 或
或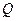 ”是真命题,求实数
”是真命题,求实数 的取值范围.
的取值范围.
1)设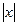 ≤1,求一个正常数a,使得x≤
≤1,求一个正常数a,使得x≤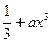 ;
;
(2)设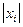 ≤1,
≤1, ,求证:
,求证: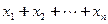 ≤
≤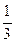
如图:空间四边形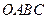 中,点
中,点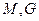 分别是
分别是 的中点.设
的中点.设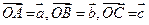
(1)用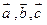 表示向量
表示向量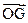 .
.
(2)若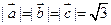 ,且
,且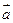 与
与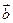 、
、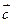 夹角的余弦值均为
夹角的余弦值均为 ,
,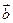 与
与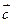 夹角为600,求
夹角为600,求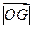
已知抛物线的顶点在坐标原点,焦点F在x轴的正半轴上,且F到抛物线的准线的距离为p.
(1) 求出这个抛物线的方程;
(2)若直线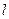 过抛物线的焦点F,交抛物线与A、B两点, 且
过抛物线的焦点F,交抛物线与A、B两点, 且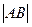 ="4p" ,求直线
="4p" ,求直线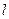 的方程.
的方程.
如果双曲线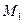 与双曲线
与双曲线 的焦点在同一坐标轴上且它们的虚轴长和实轴长的比值相等,则称他们为平行双曲线.已知双曲线M与双曲线
的焦点在同一坐标轴上且它们的虚轴长和实轴长的比值相等,则称他们为平行双曲线.已知双曲线M与双曲线 为平行双曲线,且点(2,0)在双曲线M上.
为平行双曲线,且点(2,0)在双曲线M上.
(1)求双曲线M的方程;
(2) 设P是双曲线M上的任一点,点A的坐标为(3,0),求|PA|的最小值.