足够长的粗糙斜面上，用力推着一物体沿斜面向上运动，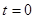
时撤去推力，0-6s内速度随时间的变化情况如图所示，由图像可知（ ）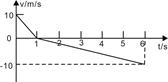
| A．0～1s内重力的平均功率大小与1～6s内重力平均功率大小之比为5∶1 |
| B．0～l s内摩擦力的平均功率与1～6s内摩擦力平均功率之比为1∶1 |
| C．0～1s内机械能变化量大小与1～6s内机械能变化量大小之比为1∶5 |
| D．1～6s内动能变化量大小与机械能变化量大小之比为1∶3 |
如图所示，以速度v沿竖直杆匀速下滑的物体A用轻绳通过定滑轮拉物体B，当绳与水平面夹角为θ时，物体B的速度为（）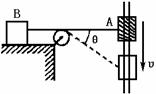
| A．v | B．v sinθ | C．v cosθ | D．v/sinθ |
某行星的质量和半径分别约为地球的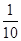
和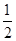
，地球表面的重力加速度为g，则该行星表面的重力加速度约为( )
| A．0.2g | B．0.4g | C．2.5g | D．5g |
对于万有引力定律的表达式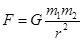
，下列说法中正确的是( )
| A．公式中G为引力常量，它是由实验测得的，而不是人为规定的 |
| B．当r趋于零时，万有引力趋于无限大 |
| C．两物体受到的引力总是大小相等的，而与m1、m2是否相等无关 |
| D．两物体受到的引力总是大小相等、方向相反，是一对平衡力 |
以下关于向心力及其作用的说法中正确的是（）
| A．向心力既改变圆周运动物体速度的方向，又改变速度的大小 |
| B．在物体所受力中，只有指向圆心的力才是向心力 |
| C．做匀速圆周运动的物体，除了受到别的物体对它的作用力外，一定还受到一个向心力的作用 |
| D．做匀速圆周运动的物体所受的合外力即为物体的向心力 |
下面说法中正确的是( )
| A．做曲线运动的物体，其速度方向必定变化 |
| B．速度变化的运动必定是曲线运动 |
| C．加速度恒定的运动不可能是曲线运动 |
| D．加速度变化的运动必定是曲线运动 |