示波器是一种多功能电学仪器,可以在荧光屏上显示出被检测的电压波形.它的工作原理等效成下列情况:如图所示,真空室中电极K发出电子(初速度不计),经过电压为U1的加速电场后,由小孔S沿水平金属板,A、B间的中心线射入板中.板长L,相距为d,在两板间加上如图乙所示的正弦交变电压,前半个周期内B板的电势高于A板的电势,电场全部集中在两板之间,且分布均匀.在每个电子通过极板的极短时间内,电场视作恒定的.在两极板右侧且与极板右端相距D处有一个与两板中心线垂直的荧光屏,中心线正好与屏上坐标原点相交.当第一个电子到达坐标原点O时,使屏以速度v沿-x方向运动,每经过一定的时间后,在一个极短时间内它又跳回到初始位置,然后重新做同样的匀速运动.(已知电子的质量为m,带电量为e,不计电子重力)求:
(1)电子进入AB板时的初速度;
(2)要使所有的电子都能打在荧光屏上,图乙中电压的最大值U0需满足什么条件?
(3)要使荧光屏上始终显示一个完整的波形,①荧光屏必须每隔多长时间回到初始位置?②计算这个波形的最大峰值和长度.③并在如图丙所示的x-y坐标系中画出这个波形.
一艘宇宙飞船绕一个不知名的、半径为R的行星表面飞行,环绕一周飞行时间为T(万有引力常量为G ),求:(1)该行星的平均密度ρ(2)该行星表面的重力加速度
如图一辆质量为500kg的汽车通过一座半径为50m的圆弧形拱桥顶部时.
(1)如果汽车以6m/s的速度经过拱桥的顶部,则汽车对圆弧形拱桥的压力是多大?
(2)如果汽车对圆弧形拱桥的压力恰好为零,则汽车通过拱桥的顶部时速度是多大?
(3)设想拱桥的半径增大到与地球半径一样,那么汽车要在这样的桥面上腾空,速度至少多大。(重力速度g取10m/s2,地球半径R取6.4×103km)
如图所示,飞机距地面高度H=500 m,水平飞行速度v1=100 m/s,追击一辆速度为v2=20 m/s同向行驶的汽车,欲使炸弹击中汽车,飞机应在距汽车水平距离多远处投弹?(g取10 m/s2).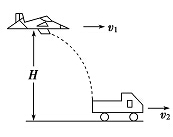
已知太阳的质量M=2.0×1030 kg,地球的质量m=6.0×1024 kg,太阳与地球相距r=1.5×1011 m,求太阳对地球的引力以及地球对太阳的引力.(G=6.67×10-11N·m2/kg2)
两个质量分别是m1、m2的人造地球卫星,分别绕地球做匀速圆周运动.若它们的轨道半径分别是R1和R2,则它们的运行周期之比是多少?