如图(1)等腰直角三角形ABC中,∠ACB=90°,直线l过点C,AD⊥l,BE⊥l,垂足分别为D、E。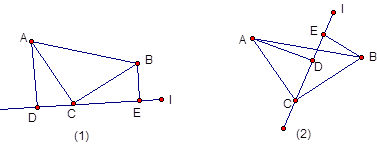
(1)求证:⊿ACD≌⊿CBE;
(2)若直线l绕点C逆时针旋转与AB相交(如图(2))且AD⊥l,BE⊥l,上述结论还成立吗?请说明理由。
如图,反比例函数y= 的图象与一次函数y=ax+b的图象交于点A(1,4),点B(m,﹣2)
的图象与一次函数y=ax+b的图象交于点A(1,4),点B(m,﹣2)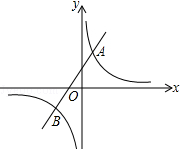
(1)求这两个函数的关系式;
(2)观察图象,写出不等式 >ax+b的解集;
>ax+b的解集;
(3)如果有一点C与点A关于x轴对称,求△ABC的面积.
为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两间工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品?
州教育局为了解我州八年级学生参加社会实践活动情况,随机抽查了某县部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据检测了两幅统计图,下面给出了两幅不完整的统计图(如图)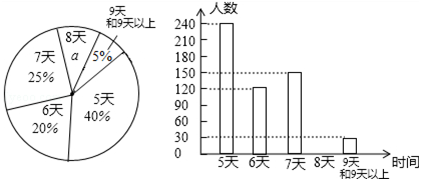
请根据图中提供的信息,回答下列问题:
(1)a= %,并写出该扇形所对圆心角的度数为 ,请补全条形图.
(2)在这次抽样调查中,众数和中位数分别是多少?
(3)如果该县共有八年级学生2000人,请你估计“活动时间不少于7天”的学生人数大约有多少人?
为了帮助农村贫困家庭子女完成初中学业,国家给他们免费提供教科书,下表是某中学免费提供教科书补助的部分情况:
| 年级 项目 |
七 |
八 |
九 |
合计 |
| 每人免费补助金额/元 |
109 |
94 |
47.5 |
﹣ |
| 人数/人 |
40 |
120 |
||
| 免费补助金额/元 |
1900 |
10095 |
求获得免费提供教科书补助的七年级和八年级的人数.
)已知:4x﹣3y﹣6z=0,x+2y﹣7z=0,且x,y,z都不为零.求 的值.
的值.