如图⑴所示的图形，像我们常见的学习用品——圆规。我们不妨把这样图形叫做“规形图”，那么在这一个简单的图形中，到底隐藏了哪些数学知识呢？下面就请你发挥你的聪明才智，解决以下问题：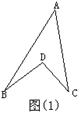
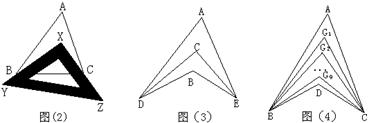
⑴观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系，并说明理由；
⑵请你直接利用以上结论，解决以下三个问题：
①如图(2)，把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、XZ恰好经过点B、C，若∠A=50°，则∠ABX+∠ACX =__________°；
②如图(3)，DC平分∠ADB, EC平分∠AEB,若∠DAE=50°，∠DBE=130°，求∠DCE的度数；
③如图（4），∠ABD，∠ACD的10等分线相交于点G1、G2
、G9，，若∠BDC=1400，∠BG1C=77°，求∠A的度数。
有A、B两个黑布袋，A布袋中有两个完全相同的小球，分别标有数字1和2．B布袋中有三个完全相同的小球，分别标有数字﹣2，﹣3和﹣4．小明从A布袋中随机取出一个小球，记录其标有的数字为x，再从B布袋中随机取出一个小球，记录其标有的数字为y，这样就确定点Q的一个坐标为（x，y）．
（1）用列表或画树状图的方法写出点Q的所有可能坐标；
（2）求点Q落在直线y=﹣x﹣2上的概率．
小英过生日，同学们为她设置了一个游戏：把三个相同的乒乓球分别标上了1、2、3，放进一个盒子摇匀，另外拿两个相同的乒乓球也分别标上1、2，放进另外一个盒子里．现从两个盒子分别抽出1个球，若两个球的数字之积为奇数，则小英唱歌，若两个球的数字之积为偶数，则小英跳舞．问：小英做哪种游戏概率大？
给你8个除颜色外完全相同的球，请你设计两个摸球游戏，分别满足：
（1）摸到红球的概率是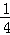
；
（2）摸到“白球或绿球”的概率是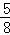
．
将6个完全相同的小球分装在甲、乙两个不透明的口袋中，甲袋中有3个球，分别标有数字1、3、5；乙袋中有3个球，分别标有数字2、4、6，从甲、乙两个口袋中各随机摸出一个球．
（1）用列表法或画树状图法，求摸出的两个球上数字之和为5的概率；
（2）摸出的两个球上数字之和为多少时的概率最大？
在一个不透明的盒子里，装有四个分别标有数字﹣2，﹣4，0，6的小球，它们的形状、大小、质地等完全相同．小明先从盒子里随机取出一个小球，记下数字为x；放回盒子摇均后，再由小华随机取出一个小球，记下数字为y．
（1）用列表法表示出（x，y）的所有可能出现的结果；
（2）求小明、小华各取一次小球所确定的点（x，y）落的二次函数y=x2+x﹣2的图象上的概率；
（3）求小明、小华各取一次小球所确定的数x、y满足y＞x2+x﹣2的概率．