(本小题满分12分)某公司有男职员45名,女职员15名,按照分层抽样的方法组建了一个4人的科研攻关小组。
(1)求某职员被抽到的概率及科研攻关小组中男、女职员的人数;
(2)经过一个月的学习、讨论,这个科研攻关组决定选出两名职员做某项实验,方法是先从小组里选出1名职员做实验,该职员做完后,再从小组内剩下的职员中选一名做实验,求选出的两名职员中恰有一名女职员的概率;
(3)实验结束后,第一次做实验的职员得到的实验数据为68,70,71,72,74,第二次做实验的职员得到的实验数据为69,70,70,72,74,请问哪位职员的实验更稳定?并说明理由。
(本小题满分14分)
已知正项数列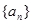 的首项
的首项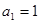 ,前
,前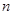 项和
项和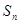 满足
满足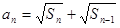
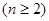 .
.
(Ⅰ)求数列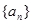 的通项公式;
的通项公式;
(Ⅱ)若数列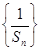 的前
的前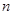 项和为
项和为 ,求证:
,求证: .
.
已知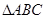 内角
内角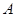 ,
,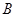 ,
,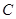 的对边分别为
的对边分别为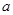 ,
, ,
,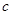 ,其中
,其中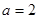 ,
,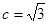 .
.
(Ⅰ)若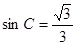 ,求
,求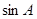 的值;
的值;
(Ⅱ)设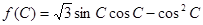 ,求
,求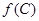 的取值范围.
的取值范围.
(本小题满分15分)
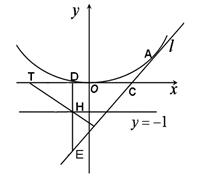
如图,已知抛物线 ,过抛物线上一点
,过抛物线上一点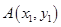 (不同于顶点)作抛物线的切线
(不同于顶点)作抛物线的切线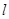 ,
,
并交 轴于点
轴于点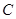 ,在直线
,在直线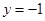 上任取一点
上任取一点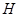 ,过
,过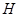 作
作 垂直
垂直 轴于点
轴于点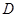 ,并交
,并交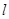 于点
于点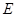 ,过
,过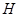 作直线
作直线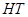 垂直于直线
垂直于直线 ,并交
,并交 轴于点
轴于点 。
。
(1)求证: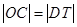 ;
;
(2)试判断直线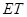 与抛物线的位置关系并说明理由.
与抛物线的位置关系并说明理由.
(本小题满分15分)已知函数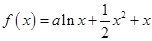 。
。
(1)求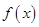 的单调区间;
的单调区间;
(2)函数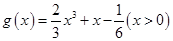 ,求证:
,求证: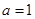 时
时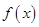 的图象都不在
的图象都不在 图象的上方.
图象的上方.
如图,三棱柱ABC—A1B1C1中,AA1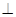 面ABC,BC
面ABC,BC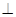 AC,BC=AC=2,D为AC的中点。
AC,BC=AC=2,D为AC的中点。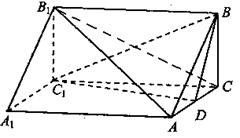
(1)若AA1=2,求证: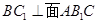 ;
;
(2)若AA1=3,求二面角C1—BD—C的余弦值.