已知椭圆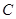 的两焦点是
的两焦点是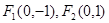 ,离心率
,离心率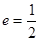 .
.
(Ⅰ)求椭圆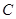 的方程;
的方程;
(Ⅱ)若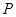 在椭圆
在椭圆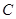 上,且
上,且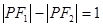 ,求DPF1F2的面积.
,求DPF1F2的面积.
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为 , ,于水面C处测得B点和D点的仰角均为 ,AC=0.1km。试探究图中B,D间距离与另外哪两点距离相等,然后求B,D的距离(计算结果精确到0.01km, 1.414, 2.449)

等比数列 的前n 项和为 ,已知 , , 成等差数列
(1)求 的公比 ;
(2)求
求


(1)已知矩阵 所对应的线性变换把点 变成点 ,试求M的逆矩阵及点A的坐标
(2)已知直线 与 试判断他们的公共点个数
(3)解不等式 .
已知函数 ,且
(1) 试用含 的代数式表示b,并求 的单调区间;
(2)令 ,设函数 在 处取得极值,记点 , , , ,请仔细观察曲线 在点P处的切线与线段MP的位置变化趋势,并解释以下问题:
(Ⅰ)若对任意的 ,线段MP与曲线 均有异于M,P的公共点,试确定t的最小值,并证明你的结论;
(Ⅱ)若存在点 , ,使得线段 与曲线 有异于 、 的公共点,请直接写出 的取值范围(不必给出求解过程)
已知A,B 分别为曲线C: 与x轴的左、右两个交点,直线 过点B,且与 轴垂直,S为 上异于点B的一点,连结AS交曲线C于点T.
(1)若曲线C为半圆,点T为圆弧 的三等分点,试求出点S的坐标;
(2)如图,点M是以SB为直径的圆与线段TB的交点,试问:是否存在 ,使得O,M,S三点共线?若存在,求出 的值,若不存在,请说明理由。
