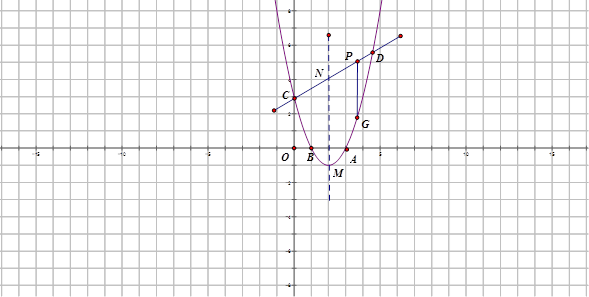
(8分)如图,抛物线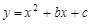 与
与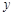 轴交于点
轴交于点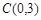 ,与
,与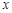 轴交于
轴交于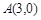 ,B两点(点A在点B的右侧),过C作直线
,B两点(点A在点B的右侧),过C作直线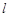 ,与抛物线相交于点
,与抛物线相交于点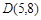 ,与对称轴交于点N,点
,与对称轴交于点N,点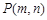 为直线
为直线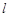 上的一个动点,过P作
上的一个动点,过P作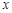 轴的垂线交抛物线于点G,设线段PG的长度为
轴的垂线交抛物线于点G,设线段PG的长度为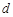
(1)求该抛物线的函数解析式
(2)当0< <5时,请用含
<5时,请用含 的代数式表示
的代数式表示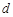 ,求出
,求出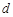 的最大值
的最大值
(3)是否存在这样的点P,使以M,N,P,G为顶点的四边形是平行四边形,若存在,请求出点P的坐标;若存在,请说明理由。
在“母亲节”前夕,我市某校学生积极参与“关爱贫困母亲”的活动,他们购进一批单价为20元的“孝文化衫”在课余时间进行义卖,并将所得利润捐给贫困母亲.经试验发现,若每件按24元的价格销售时,每天能卖出36件;若每件按29元的价格销售时,每天能卖出21件.假定每天销售件数y(件)与销售价格x(元/件)满足一个以x为自变量的一次函数.
(1)求y与x满足的函数关系式(不要求写出x的取值范围);
(2)在不积压且不考虑其他因素的情况下,销售价格定为多少元时,才能使每天获得的利润P最大?
已知 在平面直角坐标系中的位置如图所示。
在平面直角坐标系中的位置如图所示。
(1)分别写出图中点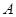 和点
和点 的坐标;
的坐标;
(2)画出 绕点A按逆时针方向旋转90°后的
绕点A按逆时针方向旋转90°后的 ;
;
(3)在(2)的条件下,求点 旋转到点
旋转到点 所经过的路线长(结果保留
所经过的路线长(结果保留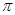 )
)
已知方程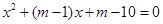 的一个根是3,求m的值及方程的另一个根.
的一个根是3,求m的值及方程的另一个根.
解方程:(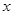 +4)2=5(
+4)2=5(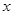 +4).
+4).
(本小题满分10分)如图,在等腰梯形ABCD中,AD∥BC,AB=DC=50,AD=75,BC=135.点P从点B出发沿折线段BA—AD—DC以每秒5个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒3个单位长的速度匀速运动,过点Q向上作射线QK⊥BC,交折线段CD—DA—AB于点E.点P,Q同时开始运动,当点P与点C重合时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).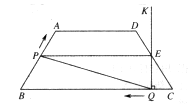
(1)当点P到达终点C时,求t的值,并指出此时BQ的长;
(2)当点P运动到AD上时,t为何值能使PQ∥DC?
(3)设射线QK扫过梯形ABCD的面积为S,分别求出点E运动到CD,DA上时,S与t的函数关系式;(不必写出t的取值范围)
(4)△PQE能否成为直角三角形?若能,写出t的取值范围;若不能,请说明理由.