为了普及环保知识,增强环保意识,某中学组织了环保知识竞赛活动,初中三个年级根据初赛成绩分别选出了10名同学参加决赛(满分为100分)如表所示:
决赛成绩(单位:分)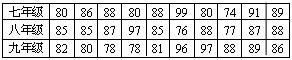
(1)请你填写下表:
(2)请从以下两个不同的角度对三个年级的决赛成绩进行分析:
从平均数和众数相结合看(分析哪个年级成绩好些): _________;
从平均数和中位数相结合看(分析哪个年级成绩好些): ___________;
(3)如果在每个年级参加决赛的选手中分别选出三人参加决赛,你认为哪个年级的实力更强一些。说明理由:__________________________________________________________。
如图,AD是⊙O的弦,AB经过圆心O,交⊙O于点C,∠DAB=∠B=30°.直线BD是否与⊙O相切?为什么?
连接CD,若CD=5,求AB的长.
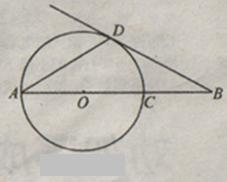
阳光中学九(1)班同学在一次综合实践活动中,对本县居民参加“全民医保”情况进行了调查,同学们利用节假日随机调查了2000人,对调查结果进行了统计分析,绘制出两幅不完整的统计图:
(注:图中A表示“城镇职工基本医疗保险”;B表示“城镇居民基本医疗保险”;C表示“新型农村合作医疗”;D表示其他情况)补全条形统计图;
在本次调查中,B类人数占被调查人数的百分比为;
据了解,国家对B类人员每人每年补助155元.已知该县人口数约80万人,请估计该县B类人员每年享受国家补助共多少万元?
图1为平地上一幢建筑物与铁塔图,图2为其示意图.建筑物AB与铁塔CD都
垂直于底面,BD=30m,在A点测得D点的俯角为45°,测得C点的仰角为60°.求铁塔CD
的高度.
如图,有牌面数字都是2,3,4的两组牌.从每组牌中各随机摸出一张,请用画树状图或列表的方法,求摸出的两张牌的牌面数字之和为6的概率. 
如图,四边形ABCD是平行四边形,EF分别是BC、AD上的点,∠1=∠2.
求证:△ABE≌△CDF.