当物体从高空下落时,所受阻力会随物体的速度增大而增大,因此经过下落一段距离后将匀速下落,这个速度称为此物体下落的收尾速度。研究发现,在相同环境条件下,球形物体的收尾速度仅与球的半径和质量有关.下表是某次研究的实验数据
| 小球编号 |
A |
B |
C |
D |
E |
| 小球的半径(×10-3m) |
0.5 |
0.5 |
1.5 |
2 |
2.5 |
| 小球的质量(×10-6kg) |
2 |
5 |
45 |
40 |
100 |
| 小球的收尾速度(m/s) |
16 |
40 |
40 |
20 |
32 |
(1)根据表中的数据,求出B球与C球在达到终极速度时所受阻力之比.
(2)根据表中的数据,归纳出球型物体所受阻力f与球的速度大小及球的半径的关系(写出有关表达式、并求出比例系数).
(3)现将C号和D号小球用轻质细线连接,若它们在下落时所受阻力与单独下落时的规律相同.让它们同时从足够高的同一高度下落,试求出它们的收尾速度;并判断它们落地的顺序.
如图所示,轻绳OA、OB、OC结于O点,A、B端挂在水平天花板下,OA=OB=10 cm,C端挂一重为10N的物体。(答案可带根号)
(1)请画出结点O的受力示意图;
(2)若∠AOB=90°,求OA绳拉力FA的大小;
(3)若轻绳OA、OB最大能承受10 N的拉力,现缓慢增大A、B两点间的距离,为了使轻绳OA、OB不断,A、B两点间的距离L不能超过多长?
某战斗机静止在地面上,若该战斗机起飞时速度为80 m/s,发动机能够提供的加速度是16 m/s2,则
(1)该战斗机从静止到起飞的时间是多少?
(2)飞机跑道长度至少要多长?
如图所示,质量M=10 kg、上表面光滑、下表面粗糙的足够长木板在F="50" N的水平拉力作用下,以初速度v0=5 m/s沿水平地面向右做匀速直线运动。现有足够多的小铁块,它们的质量均为m=0.5 kg,将一铁块无初速地放在木板的最右端,当木板运动了L=2 m时,又无初速地在木板的最右端放上第2块铁块,以后只要木板运动了L,就在木板的最右端无初速放一铁块,g取10 m/s2。求: 
(1)木板下表面与水平面间的动摩擦因数μ。
(2)第1块铁块放上后,木板的加速度的大小。
(3)第4块铁块放上的瞬间,木板的速度大小。(答案可带根号)
如图足够长的斜面倾角θ=30°。一个物体以v0=12m/s的初速度,从斜面上A点处沿斜面向上运动,加速度大小为a=8.0m/s2(g取10 m/s2)。求: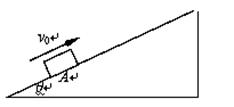
(1)物体沿斜面从A点上滑的最大距离x;
(2)物体从A点出发需经多少时间才能回到A处?
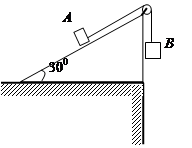
A、B两个小物块用轻绳连结,绳跨过位于倾角为30°的光滑斜面(斜面足够长)顶端的轻质滑轮,滑轮与转轴之间的摩擦不计,斜面固定在水平桌面上,如图所示.第一次,B悬空,A放在斜面上,A恰好静止;第二次,将B的质量改变,发现A自斜面顶端由静止开始运动,经时间t速度大小为v,已知物块A的质量为m,重力加速度为g,求物块B质量改变了多少?