若命题P(n)对n=k成立,则它对n=k+2也成立,又已知命题P(2)成立,则下列结论正确的是()
| A.P(n)对所有自然数n都成立 |
| B.P(n)对所有正偶数n成立 |
| C.P(n)对所有正奇数n都成立 |
| D.P(n)对所有大于1的自然数n成立 |
已知x∈R+,不等式x+ ≥2,x+
≥2,x+ ≥3,…,可推广为x+
≥3,…,可推广为x+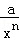 ≥n+1,则a的值为()
≥n+1,则a的值为()
| A.2n | B.n2 | C.22(n﹣1) | D.nn |
用数学归纳法证明不等式 成立,起始值至少应取为()
成立,起始值至少应取为()
| A.7 | B.8 | C.9 | D.10 |
用数学归纳法证明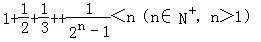 ,第二步证明从k到k+1,左端增加的项数为()
,第二步证明从k到k+1,左端增加的项数为()
| A.2k﹣1 | B.2k | C.2k﹣1 | D.2k+1 |
n条共面直线任何两条不平行,任何三条不共点,设其交点个数为f(n),则f(n+1)﹣f(n)等于()
| A.n | B.n+1 | C.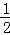 n(n﹣1) n(n﹣1) |
D.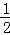 n(n+1) n(n+1) |