如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E.

(1)求证:BD=BE;
(2)若ÐDBC=30°,BO=4,求四边形ABED的面积.
如图,AB=AC,∠C=67°,AB的垂直平分线EF交AC于点D,求∠DBC的度数.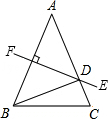
在△ABC中,AB=AC,∠A=120°,BC=9cm,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,
(1)求证:BM=MN=NC.
(2)求MN的长度.
如图,在△ABC中,已知BA=BC,∠B=120°,AB的垂直平分线DE交AC于点D.
(1)求∠A的度数;
(2)若AC=6cm,求AD的长度.
如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是点E,F,连接EF,交AD于点G,求证:AD⊥EF.
如图,在△ABC中,D、E分别是AC和AB上的点,BD与CE相交于点O,给出下列四个条件:
①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
(1)上述四个条件中,由哪两个条件可以判定AB=AC?(用序号写出所有的情形)
(2)选择(1)小题中的一种情形,说明AB=AC.