如图1，平面直角坐标系中，抛物线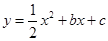
与
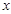轴交于A、B两点，点C是AB的中点，CD⊥AB且CD=AB.直线BE与
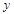轴平行，点F是射线BE上的一个动点，连接AD、AF、DF.
（1）若点F的坐标为（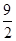
，
），AF=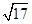
.
①求此抛物线的解析式；
②点P是此抛物线上一个动点，点Q在此抛物线的对称轴上，以点A、F、P、Q为顶点构成的四边形是平行四边形，请直接写出点Q的坐标；
（2）若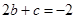
，
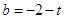，且AB的长为
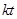，其中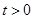
.如图2，当∠DAF=45时，求
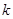的值和∠DFA的正切值.
如图，△ABC的顶点坐标分别为A（﹣6，0），B（4，0），C（0，8），把△ABC沿直线BC翻折，点A的对应点为D，抛物线y=ax2﹣10ax+c经过点C，顶点M在直线BC上．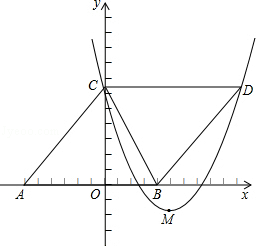
（1）证明四边形ABCD是菱形，并求点D的坐标；
（2）求抛物线的对称轴和函数表达式；
（3）在抛物线上是否存在点P，使得△PBD与△PCD的面积相等？若存在，直接写出点P的坐标；若不存在，请说明理由．
如图①，AB是半圆O的直径，以OA为直径作半圆C，P是半圆C上的一个动点（P与点A，O不重合），AP的延长线交半圆O于点D，其中OA=4．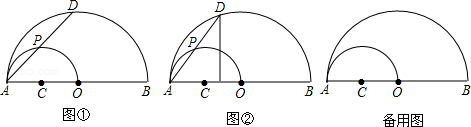
（1）判断线段AP与PD的大小关系，并说明理由；
（2）连接OD，当OD与半圆C相切时，求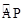
的长；
（3）过点D作DE⊥AB，垂足为E（如图②），设AP=x，OE=y，求y与x之间的函数关系式，并写出x的取值范围．
如图①，在正方形ABCD中，P是对角线AC上的一点，点E在BC的延长线上，且PE=PB．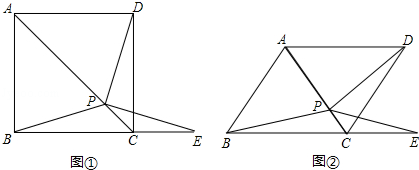
（1）求证：△BCP≌△DCP；
（2）求证：∠DPE=∠ABC；
（3）把正方形ABCD改为菱形，其它条件不变（如图②），若∠ABC=58°，则∠DPE= 度．
兴发服装店老板用4500元购进一批某款T恤衫，由于深受顾客喜爱，很快售完，老板又用4950元购进第二批该款式T恤衫，所购数量与第一批相同，但每件进价比第一批多了9元．
（1）第一批该款式T恤衫每件进价是多少元？
（2）老板以每件120元的价格销售该款式T恤衫，当第二批T恤衫售出
时，出现了滞销，于是决定降价促销，若要使第二批的销售利润不低于650元，剩余的T恤衫每件售价至少要多少元？（利润=售价﹣进价）
三张卡片的正面分别写有数字2，5，5，卡片除数字外完全相同，将它们洗匀后，背面朝上放置在桌面上．
（1）从中任意抽取一张卡片，该卡片上数字是5的概率为 ；
（2）学校将组织部分学生参加夏令营活动，九年级（1）班只有一个名额，小刚和小芳都想去，于是利用上述三张卡片做游戏决定谁去，游戏规则是：从中任意抽取一张卡片，记下数字放回，洗匀后再任意抽取一张，将抽取的两张卡片上的数字相加，若和等于7，小钢去；若和等于10，小芳去；和是其他数，游戏重新开始．你认为游戏对双方公平吗？请用画树状图或列表的方法说明理由．