在矩形ABCD中,点P在AD上,AB=2,AP=1,将三角板的直角顶点放在点P处,三角板的两直角边分别能与AB、BC边相交于点E、F,连接EF.
(1)如图,当点E与点B重合时,点F恰好与点C重合,求此时PC的长;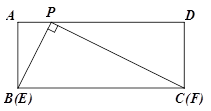
(2)将三角板从(1)中的位置开始,绕点P顺时针旋转,当点E与点A重合时停止,在这个过程中,请你观察、探究并解答: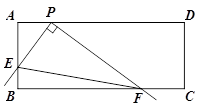
①∠PEF的大小是否发生变化?请说明理由;
②直接写出从开始到停止,线段EF的中点所经过的路线长.
如图,以 为顶点的抛物线 交 轴于 、 两点,交 轴于点 ,直线 的表达式为 .
(1)求抛物线的表达式;
(2)在直线 上有一点 ,使 的值最小,求点 的坐标;
(3)在 轴上是否存在一点 ,使得以 、 、 为顶点的三角形与 相似?若存在,请求出点 的坐标;若不存在,请说明理由.

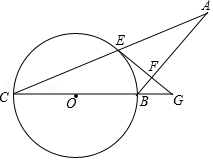
如图,在 中,以 为直径的 交 于点 ,过点 作 的垂线交 于点 ,交 的延长线于点 ,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径.
某商店销售一款进价为每件40元的护肤品,调查发现,销售单价不低于40元且不高于80元时,该商品的日销售量 (件 与销售单价 (元 之间存在一次函数关系,当销售单价为44元时,日销售量为72件;当销售单价为48元时,日销售量为64件.
(1)求 与 之间的函数关系式;
(2)设该护肤品的日销售利润为 (元 ,当销售单价 为多少时,日销售利润 最大,最大日销售利润是多少?
如图,在平行四边形 中, 是对角线 上的一点,过点 作 ,且 ,连接 、 、 .
(1)求证: ;
(2)若 ,求证:四边形 为菱形.

2017年9月,我国中小学生迎来了新版“教育部统编义务教育语文教科书”,本次“统编本”教材最引人关注的变化之一是强调对传统文化经典著作的阅读,某校对 《三国演义》、 《红楼梦》、 《西游记》、 《水浒》四大名著开展“最受欢迎的传统文化经典著作”调查,随机调查了若干名学生(每名学生必选且只能选这四大名著中的一部)并将得到的信息绘制了下面两幅不完整的统计图:
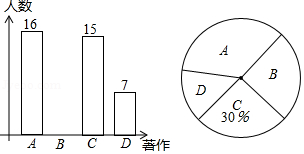
(1)本次一共调查了 名学生;
(2)请将条形统计图补充完整;
(3)某班语文老师想从这四大名著中随机选取两部作为学生暑期必读书籍,请用树状图或列表的方法求恰好选中《三国演义》和《红楼梦》的概率.