如图所示,宽度为L的金属框架竖直固定在绝缘地面上,框架的上端接有一个压敏电阻元件,其阻值与其两端所加电压成正比,即R=kU,式中k为已知的常数.框架上有一质量为m,离地高为h的金属棒,金属棒与框架始终接触良好无摩擦,且保持水平,磁感应强度为B的匀强磁场,方向垂直于框架平面向里.今将金属棒由静止释放,棒沿框架向下运动,不计金属棒电阻,重力加速度为g.试求:
(1)金属棒运动过程中,流过棒的电流大小和方向;
(2)金属棒落到地面时的速度大小;
(3)金属棒从释放到落地过程中通过电子元件的电量.
右端连有光滑弧形槽的水平桌面AB长L=1.5 m,如右图所示.将一个质量为m=0.5 kg的木块在F=1.5 N的水平拉力作用下,从桌面上的A端由静止开始向右运动,木块到达B端时撤去拉力F,木块与水平桌面间的动摩擦因数μ=0.2,取 .求:
.求:
(1)木块沿弧形槽上升的最大高度;
(2)木块沿弧形槽滑回B端后,在水平桌面上滑动的最大距离.
如下图是利用传送带装运煤块的示意图.其中,传送带足够长,倾角θ=37°,煤块与传送带间的动摩擦因数μ=0.8,传送带的主动轮和从动轮半径相等,主动轮轴顶端与运煤车底板间的竖起高度H=1.8 m,与运煤车车箱中心的水平距离x=1.2 m.现在传送带底端由静止释放一些煤块(可视为质点),煤块在传送带的作用下先做匀加速直线运动,后与传送带一起做匀速运动,到达主动轮时随轮一起匀速转动.要使煤块在轮的最高点水平抛出并落在车箱中心,取g=10 m/s2,sin 37°=0.6,cos 37°=0.8,求:
(1)传送带匀速运动的速度v及主动轮和从动轮的半径R;
(2)煤块在传送带上由静止开始加速至与传送带速度相同所经过的时间t0.
如右图所示,水平光滑绝缘轨道MN的左端有一个固定挡板,轨道所在空间存在E=4.0×102 N/C、水平向左的匀强电场.一个质量m=0.10 kg、带电荷量q=5.0×10-5 C的滑块(可视为质点),从轨道上与挡板相距x1=0.20 m的P点由静止释放,滑块在电场力作用下向左做匀加速直线运动.当滑块与挡板碰撞后滑块沿轨道向右做匀减速直线运动,运动到与挡板相距x2=0.10 m的Q点,滑块第一次速度减为零.若滑块在运动过程中,电荷量始终保持不变,求: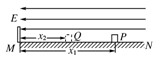
(1)滑块沿轨道向左做匀加速直线运动的加速度的大小;
(2)滑块从P点运动到挡板处的过程中,电场力所做的功;
(3)滑块第一次与挡板碰撞过程中损失的机械能.
在游乐节目中,选手需借助悬挂在高处的绳飞越到水面的浮台上,小明和小阳观看后对此进行了讨论.如下图所示,他们将选手简化为质量m=60 kg的质点,选手抓住绳由静止开始摆动,此时绳与竖直方向夹角α=53°,绳的悬挂点O距水面的高度为H=3 m.不考虑空气阻力和绳的质量,浮台露出水面的高度不计,水足够深.取重力加速度g=10 m/s2,sin 53°=0.8,cos 53°=0.6.
(1)求选手摆到最低点时对绳拉力的大小F;
(2)若绳长l=2 m,选手摆到最高点时松手落入水中.设水对选手的平均浮力Ff1=800 N,平均阻力Ff2=700 N,求选手落入水中的深度d;
(3)若选手摆到最低点时松手,小明认为绳越长,在浮台上的落点距岸边越远;小阳却认为绳越短,落点距岸边越远.请通过推算说明你的观点.
如下图所示的木板由倾斜部分和水平部分组成,两部分之间由一段圆弧面相连接.在木板的中间有位于竖直面内的光滑圆槽轨道,斜面的倾角为θ.现有10个质量均为m、半径均为r的均匀刚性球,在施加于1号球的水平外力F的作用下均静止,力F与圆槽在同一竖直面内,此时1号球球心距它在水平槽运动时的球心高度差为h.现撤去力F使小球开始运动,直到所有小球均运动到水平槽内.重力加速度为g.求: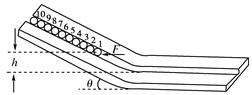
(1)水平外力F的大小;
(2)1号球刚运动到水平槽时的速度;
(3)整个运动过程中,2号球对1号球所做的功.