(本小题满分14分)
某市一家庭今年一月份、二月份和三月份煤气用量和支付费用如下表所示:
| 月份 |
用气量(立方米) |
煤气费(元) |
| 1 |
4 |
4.00 |
| 2 |
25 |
14.00 |
| 3 |
35 |
19.00 |
该市煤气收费的方法是:煤气费=基本费十超额费十保险费.
若每月用气量不超过最低额度 立方米时,只付基本费
立方米时,只付基本费 元和每户每月定额保险费
元和每户每月定额保险费 元;若用气量超过
元;若用气量超过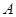 立方米时,超过部分每立方米付
立方米时,超过部分每立方米付 元.
元.
(1)根据上面的表格求 的值;
的值;
(2)记用户第四月份用气为 立方米,求他应交的煤气费
立方米,求他应交的煤气费 (元).
(元).
已知函数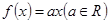 ,
,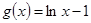 .
.
(1)若函数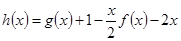 存在单调递减区间,求
存在单调递减区间,求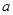 的取值范围;
的取值范围;
(2)当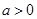 时,试讨论这两个函数图象的交点个数.
时,试讨论这两个函数图象的交点个数.
一种十字绣作品由相同的小正方形构成,图①,②,③,④分别是制作该作品前四步时对应的图案,按照如此规律,第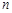 步完成时对应图案中所包含小正方形的个数记为
步完成时对应图案中所包含小正方形的个数记为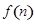 .
.
①②③④
(1)求出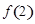 ,
,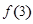 ,
, ,
, 的值;
的值;
(2)利用归纳推理,归纳出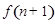 与
与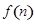 的关系式;
的关系式;
(3)猜想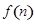 的表达式,并写出推导过程.
的表达式,并写出推导过程.
某电视台连续播放6个广告,其中有3个不同的商业广告、两个不同的宣传广告、一个公益广告,要求最后播放的不能是商业广告,且宣传广告与公益广告不能连续播放,两个宣传广告也不能连续播放,则有多少种不同的播放方式?
已知函数 的图象经过点
的图象经过点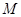 (1,4),曲线在点
(1,4),曲线在点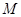 处的切线恰好与直线x+9y=0垂直.
处的切线恰好与直线x+9y=0垂直.
(1)求实数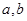 的值;
的值;
(2)若函数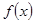 在区间
在区间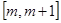 上单调递增,求
上单调递增,求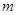 的取值范围
的取值范围
已知二次函数f(x)=ax2+bx+c,直线l1:x=2,直线l2:y=-t2+8t(其中0≤t≤2,t为常数),若直线l1,l2与函数f(x)的图象以及l1、l2、y轴与函数f(x)的图象所围成的封闭图形(阴影部分)如图所示.
(1)求a、b、c的值;
(2)求阴影面积S关于t的函数S(t)的解析式.