如图所示，一个质量为0.6 kg的小球以某一初速度从P点水平抛出，恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力，进入圆弧时无机械能损失)．已知圆弧的半径R＝0.3 m，θ＝60°，小球到达A点时的速度vA＝4 m/s.(取g＝10 m/s2)求：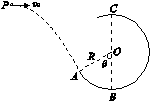
(1)小球做平抛运动的初速度v0；
(2)P点到A点的水平距离和竖直距离；
(3)小球到达圆弧最高点C时对轨道的压力．
(12分)虚线MN下方有竖直向上的匀强电场，场强大小E=2×103V/m，MN上方有一竖直长为L=0.5m的轻质绝缘杆，杆的上下两端分别固定一带电小球A、B(可看成质点)，质量均为m=0.01kg，A带电量为
；B带电量
，B到MN的距离h=0.05m。现将杆由静止释放（g取10m/s2），求：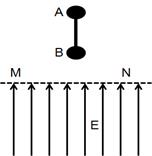
（1）小球B在匀强电场中，而A还未进入电场时，两小球的加速度大小。
（2）从开始运动到A刚要进入匀强电场过程的时间。
(12分)ABC表示竖直放在电场强度为E=104V/m的水平匀强电场中的绝缘光滑轨道，其中轨道的BC部分是半径为R的1/4圆环，轨道的水平部分与半圆环相切。A为水平轨道上的一点，而且AB=R=0.2m，把一质量m=0.1kg，带电量为
的小球，放在A点由静止释放后，求：（g=10m/s2）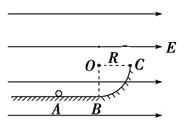
（1）小球到达C点的速度大小
（2）小球在C点时，轨道受到的压力大小
(12分)质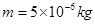量为
、电量为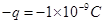
的带电微粒以2m/s的速度从水平放置的平行金属板A、B正中央水平飞入板间，已知板长L=10cm，板间距离d=2cm
（1）若带电微粒恰好沿直线穿过板间，求A、B间的电势差？（g=10m/s2）
（2）当UAB=2000V时，通过计算判断微粒能否从板间飞出？
(10分)匀强电场中，将一电量为
的负电荷由A移到B，其电势能增加了0.1J，A、B两点间距离为d=0.02m，两点连线与电场方向成60°角。求：
（1）由A移到B过程中，电场力所做的功WAB
（2）A、B两点间的电势差UAB
（3）该电场的电场强度E的大小
甲乙两运动员在训练交接棒的过程中发现:甲经短距离加速后能保持9m/s的速度跑完全程,乙从起跑后到接棒前的运动是匀加速的.为了确定乙起跑的时机.需在接力区前适当的位置设置标记.在某次练习中.甲在接力区前S0=13.5m处作了标记.并以 v=9m/s的速度跑到此标记时向乙发出起跑口令.乙在接力区的前端听到口令时起跑.并恰好在速度达到与甲相同时被甲追上.完成交接棒.已知接力区的长度为L=20m.求:
(1)此次练习中乙在接棒前得加速度a.
(2)在完成接棒时乙离接力区末端的距离.