(本小题满分12分)
已知圆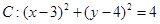 和直线
和直线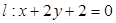 ,直线
,直线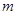 ,
,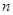 都经过圆C外定点A(1,0).
都经过圆C外定点A(1,0).
(Ⅰ)若直线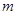 与圆C相切,求直线
与圆C相切,求直线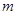 的方程;
的方程;
(Ⅱ)若直线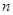 与圆C相交于P,Q两点,与
与圆C相交于P,Q两点,与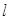 交于N点,且线段PQ的中点为M,
交于N点,且线段PQ的中点为M,
求证: 为定值.
为定值.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点。已知AB=3米,AD=2米,设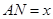 米,花坛AMPN的面积为
米,花坛AMPN的面积为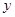 平方米
平方米
(1)求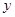 关于
关于 的函数解析式和定义域;
的函数解析式和定义域;
(2)要使花坛AMPN的面积大于32平方米,求 的取值范围;
的取值范围;
(3)当AM,AN的长度分别是多少时,花坛AMPN的面积最小,并求出最小面积.
在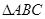 中,
中,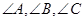 所对的边分别为
所对的边分别为 ,已知
,已知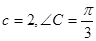
(1)若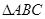 的面积为
的面积为 ,求
,求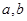 的值;
的值;
(2)求 的最大值.
的最大值.
已知直线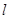 过点(1,2)且在x,y轴上的截距相等
过点(1,2)且在x,y轴上的截距相等
(1)求直线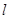 的一般方程;
的一般方程;
(2)若直线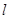 在x,y轴上的截距不为0,点
在x,y轴上的截距不为0,点 在直线
在直线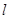 上,求
上,求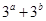 的最小值.
的最小值.
如图,四棱锥 中,底面
中,底面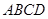 为菱形,
为菱形,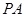 ⊥平面
⊥平面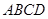 ,
, 交
交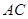 于点
于点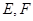 是线段
是线段 中点,
中点, 为线段
为线段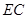 中点.
中点.
(1)求证: //平面
//平面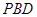 ;
;
(2)求证: ⊥
⊥ .
.
(本小题满分14分)经市场调查,某超市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间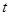 (天)的函数,且销售量近似满足
(天)的函数,且销售量近似满足 (件),价格近似满足
(件),价格近似满足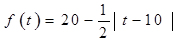 (元).
(元).
(1)试写出该种商品的日销售额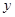 与时间
与时间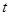 (
( )的函数关系表达式;
)的函数关系表达式;
(2)求该种商品的日销售额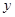 的最大值与最小值
的最大值与最小值