某民航飞机在大连海域失事,为调查失事原因,决定派海军潜水员打捞飞机上的黑匣子,如图所示,一潜水员在A处以每小时8海里的速度向正东方向划行,在A处测得黑匣子B在北偏东60°的方向,划行半小时后到达C处,测得黑匣子B在北偏东30 °的方向,在潜水员继续向东划行多少小时,距离黑匣子B最近,并求最近距离.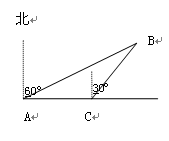
(·辽宁大连)甲乙两人制作某种机械零件.已知甲每小时比乙多做3个,甲做96个所用时间与乙做84个所用时间相等,求甲乙两人每小时各做多少个零件?
(·辽宁大连)解方程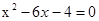
(·黑龙江绥化)某苹果生产基地,用30名工人进行采摘或加工苹果 ,每名工人只能做其中一项工作。苹果的销售方式有两种:一种是可以直接出售;另一种是可以将采摘的苹果加工成罐头出售。直接出售每吨获利4000元;加工成罐头出售每吨获利10000元。采摘的工人每人可以采摘苹果0.4吨 ;加工罐头的工人每人可加工0.3吨。设有x名工人进行苹果采摘 ,全部售出后,总利润为y元 .
(1)求y与x的函数关系式。
(2)如何分配工人才能活力最大
(·黑龙江绥化)自学下面材料后,解答问题。
分母中含有未知数的不等式叫分式不等式。如: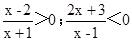 等 。那么如何求出它们的解集呢?
等 。那么如何求出它们的解集呢?
根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负。其字母表达式为:
(1)若a>0 ,b>0 ,则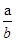 >0;若a<0 ,b<0,则
>0;若a<0 ,b<0,则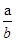 >0;
>0;
(2)若a>0 ,b<0 ,则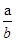 <0 ;若a<0,b>0 ,则
<0 ;若a<0,b>0 ,则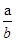 <0。
<0。
反之:(1)若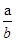 >0则
>0则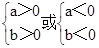
(2)若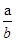 <0 ,则__________或_____________.
<0 ,则__________或_____________.
根据上述规律,求不等式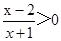 的解集。
的解集。
(·辽宁丹东)先化简,再求值: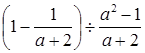 ,其中,
,其中,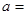 3.
3.