某商场购进一批单价为50元的商品,规定销售时单价不低于进价,每件的利润不超过40%.其中销售量y(件)与所售单价x(元)的关系可以近似的看作如图所表示的一次函数.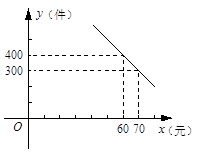
(1)求y与x之间的函数关系式,并求出x的取值范围;
(2)设该公司获得的总利润(总利润=总销售额-总成本)为w元,求w与x之间的函数关系式.当销售单价为何值时,所获利润最大?最大利润是多少?
为了维护国家主权和海洋权利,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在 处测得灯塔 在北偏东 方向上,继续航行1小时到达 处,此时测得灯塔 在北偏东 方向上.
(1)求 的度数;
(2)已知在灯塔 的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?

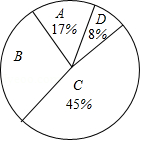
为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表.
|
组别 |
分数段 |
频次 |
频率 |
|
|
|
17 |
0.17 |
|
|
|
30 |
|
|
|
|
|
0.45 |
|
|
|
8 |
0.08 |
请根据所给信息,解答以下问题:
(1)表中 , ;
(2)请计算扇形统计图中 组对应扇形的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率.
解不等式组 ,并把它的解集在数轴上表示出来.
已知抛物线 的顶点为 ,与 轴的交点为 .
(1)求 的解析式;
(2)若直线 与 仅有唯一的交点,求 的值;
(3)若抛物线 关于 轴对称的抛物线记作 ,平行于 轴的直线记作 .试结合图形回答:当 为何值时, 与 和 共有:①两个交点;②三个交点;③四个交点;
(4)若 与 轴正半轴交点记作 ,试在 轴上求点 ,使 为等腰三角形.

为了丰富同学们的课余生活,某学校计划举行“亲近大自然”户外活动,现随机抽取了部分学生进行主题为“你最想去的景点是?”的问卷调查,要求学生必须从“ (洪家关), (天门山), (大峡谷), (黄龙洞)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.

请你根据图中所提供的信息,完成下列问题:
(1)本次调查的学生人数为 ;
(2)在扇形统计图中,“天门山”部分所占圆心角的度数为 ;
(3)请将两个统计图补充完整;
(4)若该校共有2000名学生,估计该校最想去大峡谷的学生人数为 .