已知函数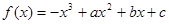 图像上的点
图像上的点 处的切线方程为
处的切线方程为 .
.
(1)若函数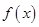 在
在 时有极值,求
时有极值,求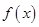 的表达式;
的表达式;
(2)函数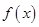 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围.
已知圆 过定点
过定点 ,圆心
,圆心 在抛物线
在抛物线 上,
上, 、
、 为圆
为圆 与
与 轴的交点.
轴的交点.
(Ⅰ)当圆心 是抛物线的顶点时,求抛物线准线被该圆截得的弦长.
是抛物线的顶点时,求抛物线准线被该圆截得的弦长.
(Ⅱ)当圆心 在抛物线上运动时,
在抛物线上运动时, 是否为一定值?请证明你的结论.
是否为一定值?请证明你的结论.
(Ⅲ)当圆心 在抛物线上运动时,记
在抛物线上运动时,记 ,
, ,求
,求 的最大值,并求出此时圆
的最大值,并求出此时圆 的方程.
的方程.
已知等比数列 中,
中, ,公比
,公比 ,
, 又恰为一个等差数列的第7项,第3项和第1项.
又恰为一个等差数列的第7项,第3项和第1项.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列
如图,在三棱锥 中,直线
中,直线 平面
平面 ,且
,且 ,又点
,又点 ,
, ,
, 分别是线段
分别是线段 ,
, ,
, 的中点,且点
的中点,且点 是线段
是线段 上的动点.
上的动点.
(1)证明:直线 平面
平面 ;
;
(2)若 ,求二面角
,求二面角 的平面角的余弦值.
的平面角的余弦值.
已知函数 ,x∈R.
,x∈R.
(1)求函数f(x)的最小正周期及对称轴方程;
(2)当 时,求函数f(x)的最大值和最小值及相应的x值.
时,求函数f(x)的最大值和最小值及相应的x值.
已知圆心在第二象限内,半径为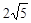 的圆
的圆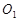 与
与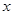 轴交于
轴交于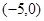 和
和 两点.
两点.
(1)求圆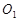 的方程;
的方程;
(2)求圆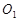 的过点A(1,6)的切线方程;
的过点A(1,6)的切线方程;
(3)已知点N(9,2)在(2)中的切线上,过点A作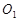 N的垂线,垂足为M,点H为线段AM上异于两个端点的动点,以点H为中点的弦与圆交于点B,C,过B,C两点分别作圆的切线,两切线交于点P,求直线
N的垂线,垂足为M,点H为线段AM上异于两个端点的动点,以点H为中点的弦与圆交于点B,C,过B,C两点分别作圆的切线,两切线交于点P,求直线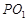 的斜率与直线PN的斜率之积.
的斜率与直线PN的斜率之积.