解方程：
（1）
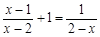（2）
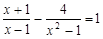
我县实施新课程改革后，学生的自主字习、合作交流能力有很大提高．张老师为了了解所教班级学生自主学习、合作交流的具体情况，对本班部分学生进行了为期半个月的跟踪调査，并将调査结果分成四类，A：特别好；B：好；C：一般；D：较差；并将调査结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：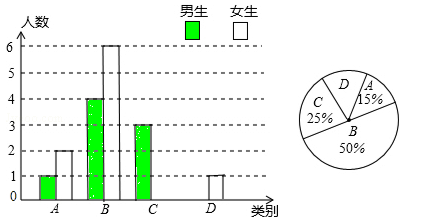
（1）本次调查中，张老师一共调査了 名同学，其中C类女生有 名，D类男生有 名；
（2）将上面的条形统计图补充完整；
（3）为了共同进步，张老师想从被调査的A类和D类学生中分别选取一位同学进行“一帮一”互助学习，请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率．
计算：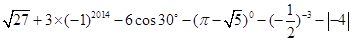
；
（2）先化简再求值：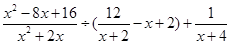
，其中x为该不等式组
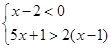的整数解．
如图，二次函数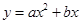
（
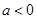）的图象过坐标原点O，与x轴的负半轴交于点A，过A点的直线与y轴交于B，与二次函数的图象交于另一点C，且C点的横坐标为﹣1，AC：BC=3：1．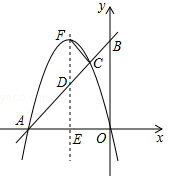
（1）求点A的坐标；
（2）设二次函数图象的顶点为F，其对称轴与直线AB及x轴分别交于点D和点E，若△FCD与△AED相似，求此二次函数的关系式．
探究：如图①，在△ABC中，AB=AC，∠ABC=60°，延长BA至点D，延长CB至点E，使BE=AD，连结CD，AE，求证：△ACE≌△CBD．
应用：如图②，在菱形ABCF中，∠ABC=60°，延长BA至点D，延长CB至点E，使BE=AD，连结CD，EA，延长EA交CD于点G，求∠CGE的度数．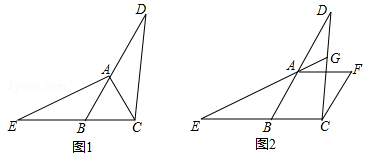
学校计划选购甲、乙两种图书作为“校园读书节”的奖品．已知甲图书的单价是乙图书单价的1.5倍；用600元单独购买甲种图书比单独购买乙种图书要少10本．
（1）甲、乙两种图书的单价分别为多少元？
（2）若学校计划购买这两种图书共40本，且投入的经费不超过1050元，要使购买的甲种图书数量不少于乙种图书的数量，则共有几种购买方案？