椭圆 上有n个不同的点:P1,P2, ,Pn,椭圆的右焦点为F,数列{|PnF|}是公差大于
上有n个不同的点:P1,P2, ,Pn,椭圆的右焦点为F,数列{|PnF|}是公差大于 的等差数列,则n的最大值是 ( )
的等差数列,则n的最大值是 ( )
| A.198 | B.199 |
| C.200 | D.201 |
若 在
在 上是减函数,则b的取值范围是()
上是减函数,则b的取值范围是()
A. |
B. |
C. |
D. |
《张丘建算经》卷上第22题为:今有女善织,日益功疾,且从第2天起,每天比前一天多织相同量的布,若第1天织5尺布,现在一月(按30天计)共织390尺布,则每天比前一天多织________尺布。(不作近似计算)()
A. |
B. |
C. |
D. |
 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 ,则
,则 ()
()
| A.4 | B. |
C.3 | D. |
我们把具有以下性质的函数 称为“好函数”:对于在
称为“好函数”:对于在 定义域内的任意三个数
定义域内的任意三个数 ,若这三个数能作为三角形的三边长,则
,若这三个数能作为三角形的三边长,则 也能作为三角形的三边长.现有如下一些函数:
也能作为三角形的三边长.现有如下一些函数:
①
②
③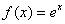 ,
,
④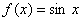 ,
, .
.
其中是“好函数”的序号有()
| A.①② | B.①②③ | C.②③④ | D.①③④ |
已知 满足约束条件
满足约束条件 ,当目标函数
,当目标函数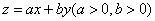 在约束条件下取到最小值
在约束条件下取到最小值 时,
时, 的最小值为()
的最小值为()
| A.1 | B.2 | C.3 | D.4 |