（本小题8分）某中学拟组织九年级师生去泰山举行毕业联欢活动．下面是年级组长李老师和小芳、小明同学有关租车问题的对话：
李老师：“平安客运公司有
座和
座两种型号的客车可供租用，座客车每辆每天的租金比座的贵
元．”
小芳：“我们学校八年级师生昨天在这个客运公司租了
辆座和
辆座的客车到泰山参观，一天的租金共计
元．”
小明：“我们九年级师生租用
辆座和
辆45座的客车正好坐满．”
根据以上对话，解答下列问题：
（1）平安客运公司
座和座的客车每辆每天的租金分别是多少元？
（2）按小明提出的租车方案，九年级师生到该公司租车一天，共需租金多少元？
计算:（1）
；（2）
；
（3）
.
；（4）
÷
你能求（x—1）（x99+x98+x97+……+x+1）的值吗？
遇到这样的问题，我们可以先思考一下，从简单的情形入手。分别计算下列各式的值：
（1）(x—1)(x+1)=x2－1；
（2）(x—1)(x2+x+1)= x3－1；
（3）(x—1)(x3+x2+x+1)= x4－1；
……
由此我们可以得到：
（x—1）（x99+x98+x97+……+x+1）=____________；
请你利用上面的结论，完成下面两题的计算：
（1）299+298+297+……+2+1；
（2）（—2）50+（—2）49+（—2）48+……+（－2）+1.
如图，O是△ABC的3条角平分线的交点，0G⊥BC，垂足为G．
（1）猜想：∠BOC与∠BAC之间的数量关系，并说明理由；
（2）∠DOB与∠GOC相等吗?为什么?
要使方程组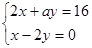
有正整数解，求整数
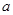的值。
如图，把一张边长为xcm的正方形纸板的四个角各剪去一个边长为ycm的小正方形，然后把它折成一个无盖纸盒，求纸盒的四个侧面的面积之和（结果用关于x、y的代数式表示）．