如图所示，平板车长为L=6m，质量为M=10kg，上表面距离水平地面高为h=1.25m，在水平面上向右做直线运动，A、B是其左右两个端点．某时刻小车速度为v0=7.2m/s，在此时刻对平板车施加一个方向水平向左的恒力F=50N，与此同时，将一个质量m=1kg为小球轻放在平板车上的P点（小球可视为质点，放在P点时相对于地面的速度为零），PB长度为L的三分之一，经过一段时间，小球脱离平板车落到地面．车与地面的动摩擦因数为0.2，其他摩擦均不计．取g=10m/s2．求：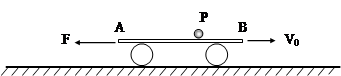
（1）小球从离开平板车开始至落到地面所用的时间；
（2）小球从轻放到平板车开始至离开平板车所用的时间；
（3）从小球轻放上平板车到落地瞬间，平板车的位移大小．
质量为O.02kg的小球，用细线拴着吊在沿直线行驶的汽车的顶棚上，在汽车距车站15 m处开始刹车，在刹车过程中,栓小球的细线与竖直方向夹角37o保持不变，如图所示，汽车到站恰好停止。求:①刹车过程中细线对小球的拉力。②开始刹车时汽车的速度。(g取10m／s2，sin37o=O.6，cos37o=O.8)
一个质量为4kg的物体静止在足够大的水平地面上，物体与地面间的动摩擦因数μ=0.1。从t=0开始，物体受到一个大小和方向呈周期性变化的水平力F作用，力F随时间的变化规律如图所示。（g取10m/s2）求：
①0到2s和2s到4s的加速度。
②83秒内物体的位移大小。
如图所示，物体从光滑斜面上的A点由静止开始下滑，经过B点后进入水平面（设经过B点前后速度大小不变），最后停在C点。每隔0.2秒钟通过速度传感器测量物体的瞬时速度，下表给出了部分测量数据。（重力加速度g＝10m/s2）求：
①斜面的倾角a；②物体与水平面之间的动摩擦因数m；
如图所示，某货场而将质量为m1="100" kg的货物（可视为质点）从高处运送至地面，为避免货物与地面发生撞击，现利用固定于地面的光滑四分之一圆轨道，使货物从轨道顶端无初速滑下，设货物滑到底端即在A最左端时货物的速度V0=6m/s。地面上紧靠轨道次排放两个完全相同的木板A、B，长度均为l=2m，质量均为m2="100" kg，木板上表面与轨道末端相切。货物与木板间的动摩擦因数为
1，木板与地面间的动摩擦因数=0.2。（最大静摩擦力与滑动摩擦力大小相等，取g="10" m/s2）
①若1=0.5，且货物滑上木板A时，木板不动，求货物滑到木板A末端时的速度和在木板A上运动的时间。
②若要使货物滑上木板A时，木板不动，而滑上木板B时，木板B开始滑动，求1应满足的条件。
质量为O.02kg的小球，用细线拴着吊在沿直线行驶的汽车的顶棚上，在汽车距车站15 m处开始刹车，在刹车过程中,栓小球的细线与竖直方向夹角37o保持不变，如图所示，汽车到站恰好停止。求:①刹车过程中细线对小球的拉力。②开始刹车时汽车的速度。(g取10m／s2，sin37o=O.6，cos37o=O.8)