用反证法证明命题:“一个三角形中不能有两个直角”的过程归纳为以下三个步骤:
① ,这与三角形内角和为
,这与三角形内角和为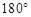 相矛盾,
相矛盾, 不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角
不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角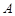 、
、 、
、 中有两个直角,不妨设
中有两个直角,不妨设 ,正确顺序的序号为
,正确顺序的序号为
| A.①②③ | B.③①② | C.①③② | D.②③① |
设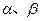 为两个不同的平面,m、n为两条不同的直线,且m
为两个不同的平面,m、n为两条不同的直线,且m
 ,n
,n
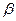 ,有如下的两个命题:p:若
,有如下的两个命题:p:若 //
//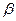 ,则m//n;q:若m
,则m//n;q:若m n,则
n,则

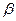 .那么
.那么
| A.“p或q”是假命题 | B.“p且q”是真命题 |
| C.“非p或q”是假命题 | D.“非p且q”是真命题 |
函数f(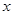 )=
)=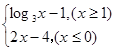 的反函数是
的反函数是
A.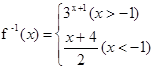 |
B. |
C.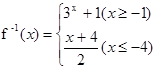 |
D.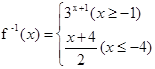 |
(文)已知集合S={ <0},T= {
<0},T= {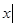 x2-(2a+1)
x2-(2a+1) +a2+a
+a2+a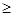 0}(a
0}(a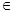 R),则S∪T=R的充要条件是
R),则S∪T=R的充要条件是
| A.-1≤a≤1 | B.-1<a≤1 | C.0<a≤1 | D.0≤a≤1 |
(理)若 =a+bi(a,b
=a+bi(a,b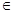 R,i是虚数单位),则a-b等于
R,i是虚数单位),则a-b等于
| A.-7 | B.-1 | C.-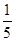 |
D.-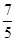 |
已知等差数列{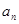 }的前
}的前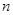 项和为
项和为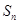 ,且
,且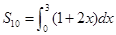 ,
, ,则
,则 为
为
()
A. |
B. |
C.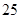 |
D.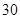 |