如图,抛物线 与
与 轴交于点A(-1,0)、B(3,0),与
轴交于点A(-1,0)、B(3,0),与 轴交于点C(0,3).
轴交于点C(0,3).
(1)求抛物线的解析式及顶点D的坐标;
(2)若P为线段BD上的一个动点,点P的横坐标为m,试用含m的代数式表示点P的纵坐标;
(3)过点P作PM⊥x轴于点M,求四边形PMAC的面积的最大值和此时点P的坐标;
(4)若点F是第一象限抛物线上的一个动点,过点F作FQ∥AC交x轴于点Q.当点F的坐标为 时,四边形FQAC是平行四边形;当点F的坐标为 时,四边形FQAC是等腰梯形(直接写出结果,不写求解过程).
计算: .
.
如图,在平面直角坐标系中,直线y=﹣2x+42交x轴于点A,交直线y=x于点B,抛物线y=ax2﹣2x+c分别交线段AB、OB于点C、D,点C和点D的横坐标分别为16和4,点P在这条抛物线上.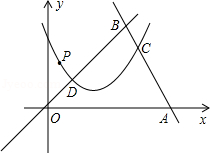
(1)求点C、D的纵坐标.
(2)求a、c的值.
(3)若Q为线段OB上一点,P、Q两点的纵坐标都为5,求线段PQ的长.
(4)若Q为线段OB或线段AB上一点,PQ⊥x轴,设P、Q两点间的距离为d(d>0),点Q的横坐标为m,直接写出d随m的增大而减小时m的取值范围.
如图,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3.
(1)求抛物线所对应的函数解析式;(2)求△ABD的面积(3)将△AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由.
某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元;市场调查发现,若每箱以45元的价格销售,平均每天销售105箱;每箱以50元的价格销售,平均每天销售90箱.假定每天销售量y(箱)与销售价x(元/箱)之间满足一次函数关系式.
(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式;
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式;
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
如图,在单位长度为1的正方形网格中,一段圆弧经过格点A、B、C.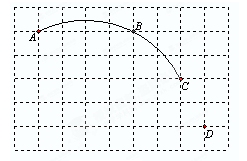
(1)请找出该圆弧所在圆的圆心O的位置;
(2)请在(1)的基础上,完成下列问题:
①⊙O的半径为_______(结果保留根号);
②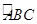 的长为_________(结果保留π);
的长为_________(结果保留π);
③试判断直线CD与⊙O的位置关系,并说明理由.