已知数列 的各项均为正数,且满足
的各项均为正数,且满足 ,
, .
.
(1)推测 的通项公式;
的通项公式;
(2)若 ,令
,令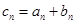 ,求数列
,求数列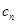 的前
的前 项和
项和
某企业要建造一个容积为18m3,深为2m的长方体形无盖贮水池,如果池底和池壁每平方米的造价分别为200元和150元,怎样设计该水池可使得能总造价最低?最低总造价为多少?
已知以点C(1,﹣2)为圆心的圆与直线x+y﹣1=0相切.
(1)求圆C的标准方程;
(2)求过圆内一点P(2,﹣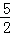 )的最短弦所在直线的方程.
)的最短弦所在直线的方程.
在△ABC中,角A,B,C所对的边分别为a,b,c,已知b=3,c=8,角A为锐角,△ABC的面积为6 .
.
(1)求角A的大小;
(2)求a的值.
已知三角形的三个顶点是A(4,0),B(6,6),C(0,2).
(1)求AB边上的高所在直线的方程;
(2)求AC边上的中线所在直线的方程.
设各项为正数的数列 的前
的前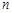 和为
和为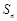 ,且
,且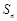 满足:
满足: .等比数列
.等比数列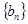 满足:
满足: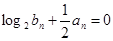 .
.
(Ⅰ)求数列 ,
,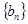 的通项公式;
的通项公式;
(Ⅱ)设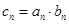 ,求数列
,求数列 的前
的前 项的和
项的和 ;
;
(Ⅲ)证明:对一切正整数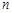 ,有
,有 .
.