(本小题满分15分)
已知函数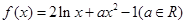
(Ⅰ)求函数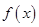 的单调区间;
的单调区间;
(Ⅱ)若 ,试分别解答以下两小题.
,试分别解答以下两小题.
(ⅰ)若不等式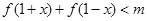 对任意的
对任意的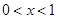 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(ⅱ)若 是两个不相等的正数,且
是两个不相等的正数,且 ,求证:
,求证: .
.
已知焦点在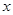 轴上的椭圆
轴上的椭圆 和双曲线
和双曲线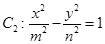 的离心率互为倒数,它们在第一象限交点的坐标为
的离心率互为倒数,它们在第一象限交点的坐标为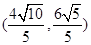 ,设直线
,设直线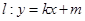 (其中
(其中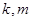 为整数).
为整数).
(1)试求椭圆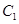 和双曲线
和双曲线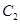 的标准方程;
的标准方程;
(2)若直线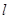 与椭圆
与椭圆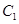 交于不同两点
交于不同两点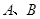 ,与双曲线
,与双曲线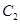 交于不同两点
交于不同两点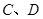 ,问是否存在直线
,问是否存在直线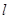 ,使得向量
,使得向量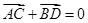 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
已知函数 与
与 的图像都过点
的图像都过点 ,且它们在点
,且它们在点 处有公共切线.
处有公共切线.
(1)求函数 和
和 的表达式及在点
的表达式及在点 处的公切线方程;
处的公切线方程;
(2)设 ,其中
,其中 ,求
,求 的单调区间.
的单调区间.
如图,三棱柱 的侧棱与底面
的侧棱与底面 垂直,底面
垂直,底面 是等腰直角三角形,
是等腰直角三角形, ,侧棱
,侧棱 ,
, 分别是
分别是 与
与 的中点,点
的中点,点 在平面
在平面 上的射影是
上的射影是 的垂心
的垂心

(1)求证: ;
;
(2)求 与平面
与平面 所成角的大小.
所成角的大小.
选聘高校毕业生到村任职,是党中央作出的一项重大决策,这对培养社会主义新农村建设带头人、引导高校毕业生面向基层就业创业,具有重大意义。为了响应国家号召,某大学决定从符合条件的6名(其中男生4人,女生2人)报名大学生中选择3人,到某村参加村委会主任应聘考核。
(Ⅰ)设所选3人中女生人数为 ,求
,求 的分布列及数学期望;
的分布列及数学期望;
(Ⅱ)在男生甲被选中的情况下,求女生乙也被选中的概率.
如图,倾斜角为 的直线
的直线 与单位圆在第一象限的部分交于点
与单位圆在第一象限的部分交于点 ,单位圆与坐标轴交于点
,单位圆与坐标轴交于点 ,点
,点 ,
, 与
与 轴交于点
轴交于点 ,
, 与
与 轴交于点
轴交于点 ,设
,设


(1)用角 表示点
表示点 、点
、点 的坐标;
的坐标;
(2)求 的最小值.
的最小值.