已知点 为
为 轴上的动点,点
轴上的动点,点 为
为 轴上的动点,点
轴上的动点,点 为定点,且满足
为定点,且满足 ,
, .
.
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过点 且斜率为
且斜率为 的直线
的直线 与曲线
与曲线 交于两点
交于两点 ,
, ,试判断在
,试判断在 轴上是否存在点
轴上是否存在点 ,使得
,使得 成立,请说明理由.
成立,请说明理由.
某企业生产一种产品时,固定成本为5000元,而每生产100台产品时直接消耗成本要增加2500元,市场对此商品年需求量为500台,销售的收入函数为R(x)=5x-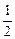 x2(万元)(0≤x≤5),其中x是产品售出的数量(单位: 百台)
x2(万元)(0≤x≤5),其中x是产品售出的数量(单位: 百台)
(1)把利润表示为年产量的函数;
(2)年产量多少时,企业所得的利润最大?
(3)年产量多少时,企业才不亏本?
一个小服装厂生产某种风衣,月销售量x(件)与售价P(元/件)之间的关系为P=160-2x,生产x件的成本R=500+30x元

(1)该厂的月产量多大时,月获得的利润不少于1300元?
(2)当月产量为多少时,可获得最大利润?最大利润是多少元?
二次函数f(x)=px2+qx+r中实数p、q、r满足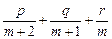 =0,其中m>0,求证:
=0,其中m>0,求证:
(1)pf(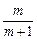 )<0;
)<0;
(2)方程f(x)=0在(0,1)内恒有解.
如果二次函数y=mx2+(m-3)x+1的图象与x轴的交点至少有一个在原点的右侧,试求m的取值范围.
已知实数t满足关系式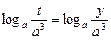 (a>0且a≠1)
(a>0且a≠1)
(1)令t=ax,求y=f(x)的表达式;
(2)若x∈(0,2 时,y有最小值8,求a和x的值.
时,y有最小值8,求a和x的值.