为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.下表是该市居民“一户一表”生活用水及提示计费价格表的部分信息:
| |
自来水销售价格 |
污水处理价格 |
| 每户每月用水量 |
单价:元/吨 |
单价:元/吨 |
| 17吨以下 |
a |
0.80 |
| 超过17吨但不超过30吨的部分 |
b |
0.80 |
| 超过30吨的部分 |
6.00 |
0.80 |
(说明:①每户产生的污水量等于该户自来水用水量;②水费=自来水费用+污水处理费用)
已知小王家2013年1月份用水20吨,交水费66元;2月份用水25吨,交水费91元.
(1)求a、b的值;
(2)随着夏天的到来,用水量将增加.为了节省开支,小王计划把6月份的水费控制在不超过家庭月收入的2%.若小王家的月收入为9200元,则小王家6月份最多能用水多少吨?
某中学团委会为研究该校学生的课余活动情况,采取抽样的方法,从阅读.运动.娱乐.其它等四个方面调查了若干名学生的兴趣爱好,并将调查的结果绘制了如下的两幅不完整的统计图(如图),请你根据图中提供的信息解答下列问题: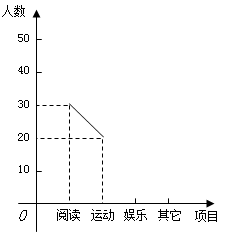

(1)在这次研究中,一共调查了多少名学生?
(2)“其它”在扇形图中所占的圆心角是多少度?
(3)补全频数分布折线图.
某市有5类学校,各类学校占总校数的百分比如下:
| 学校 |
幼儿园 |
小学 |
中学 |
特殊教育 |
高等院校 |
| 百分比 |
36% |
32% |
22% |
4% |
6% |
(1)计算各类学校对应的扇形圆心角度数;
(2)画扇形统计图来表示上面的信息;
(3)哪两类学校较多?各占百分比是多少?
(4)若高等院校有42所,则该市共有学校多少所?中学有多少所?
社会的信息化程度越来越高,计算机网络已进人普通百姓家,某市电信局对计算机拨号上网用户提供三种付费方式供用户选择(每个用户只能选择其中一种付费方式):甲种方式是按实际用时付费,每小时付信息费4元,另加付电话话费每小时1元2角;乙种方式是包月制,每月付信息费100元,同样另加付电话话费每小时1元2角;丙种方式也是包月制,每月付信息费150元,但不必另付电话费.某用户为选择合适的付费方式,连续记录了7天中每天上网所花的时间(单位:分):
| 第一天 |
第二天 |
第三天 |
第四天 |
第五天 |
第六天 |
第七天 |
|
| 上网时间 |
62 |
40 |
35 |
74 |
27 |
60 |
80 |
根据上述情况,该用户选择哪种付费方式比较合适,请你帮助选择,并说明理由(每个月按30天计)
为了保护环境,某校环保小组成员小明收集废电池,第一天收集1号电池4节,5号电池5节,总重量为450克,第二天收集1号电池2节,5号电池3节,总重量为240克。
(1)求1号电池和5号电池每节分别重多少?
(2)学校环保小组为估算四月份收集废电池的总重量,他们随意抽取了该月某5天每天收集废电池的数量,如下表:
| 1号废电池(单位:节) |
29 |
30 |
32 |
28 |
31 |
| 5号废电池(单位:节) |
51 |
53 |
47 |
49 |
50 |
分别计算两种废电池的样本平均数;并由此估算该月(30天)环保小组收集废电池的总重量是多少千克?
(3)试说明上述表格中数据的获取方法。你认为这种方法合理吗?
《红楼梦》是我国最经典的名著之一,为了了解我国阅读过,《红楼梦》的读者,你认为采用什么方式调查更合适些?你认为对不同地区,不同年龄,不同文化背景的人所做的调查结果会一样吗?