给出定义：若函数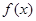
在D上可导，即
存在，且导函数在D上也可导，则称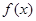在D上存在二阶导函数，记
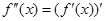，若
> 0在D上恒成立，则称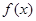在D上为凹函数，以下四个函数在
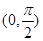上是凹函数的是( )
A． |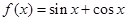
B． |
C． |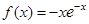
D． |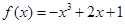
如图是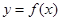函数
的导函数
的图象，给出下列命题：①-2是函数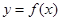的极值点；②1是函数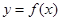的最小值点；③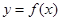在
处切线的斜率小于
零；④在区间（-2，2）上单调递增.则正确命题的序号是( )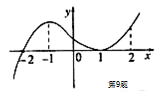
| A．①④ | B．②④ | C．③④ | D．②③ |
按如图所求示的程序框图运算，若输入的x值为2，则输出的k值是（）
| A．3 | B．4 | C．5 | D．6 |
已知
是两个不同的平面，m，n是两条不同的直线，给出下列命题：( )
①若
；
②若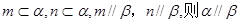
；
③如果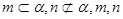
是异面直线，那么
与
相交；
④若
且
，则
且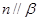
其中正确的命题是（）
| A．①② | B．①④ | C．②③ | D．③④ |
已知实数
满足
则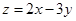
的最大值是( )
A． |
B． |
C． |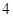
D． |
的渐近线方程为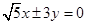
则双曲线的一个焦点F到渐近线的距离为（）
| A．2 | B． |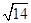
C． |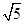
D． ． |