某篮球队运动员进行3分球投篮成绩测试,每人每天投3分球10次,对甲、乙两名队员在5天中进球的个数统计如果如下:
| 队员 |
每人每天进球数 |
||||
| 甲 |
10 |
6 |
10 |
8 |
8 |
| 乙 |
9 |
9 |
7 |
8 |
9 |
经计算,甲进球的平均数为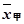
=8.4和方差s甲2="2.24."
(1)求乙进球的平均数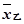
和方差s乙2;
(2)现在需要根据以上结果,从甲、乙二人中选出一人去参加3分球投篮大赛,你认为应该选哪名队员?为什么?
的解集为
，求
的值．
的立方根是3，16的算术平方根是
，求：
、
的值；
的平方根．
，
，试求
的值．
并将其解集在数轴上表示出来．
